Time Series Analysis and Examples

Getting Started

The fractional differencing enables the degree of differencing d to take any real value rather than being restricted to integer values. The fractionally differenced processes are capable of modeling long-term persistence. The process

$(1-B)^ dy_{t} = {\epsilon }_ t$

is known as a fractional Gaussian noise process or an ARFIMA(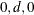 $0,d,0$ ) process, where 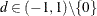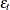$d\in (-1,1) \backslash \{ 0\}$ , $\epsilon _ t$ is a white noise process with mean 0 and variance 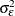$\sigma _{\epsilon }^2$ , and B is the backshift operator such that 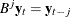$B^ j\mb{y}_{t}=\mb{y}_{t-j}$ . An ARFIMA( 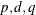$p,d,q$ ) model extends the ARFIMA( 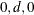$0,d,0$ ) model and combines fractional differencing with an ARMA( 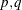$p,q$ ) model.

Consider an ARFIMA(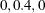 $0,0.4,0$ ) model that is represented as 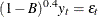$(1-B)^{0.4}y_{t} = {\epsilon }_ t$ , where 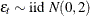$\epsilon _ t \sim \mr{iid} ~ N(0, 2)$ . The following statements accomplish several tasks:

generate 300 observations of simulated data
obtain the fractionally differenced data
compute the autocovariance function
compute the log-likelihood function
fit a fractionally integrated time series model to the data

The output is shown in Output 14.14 through Output 14.18.

proc iml;
/* ARFIMA(0,0.4,0) */
lag = (0:12)`;
call farmacov(autocov_D_IS_04, 0.4);
call farmacov(D_IS_005, 0.05);
print lag autocov_D_IS_04 D_IS_005;

d = 0.4;
call farmasim(yt, d) n=300 sigma=2 seed=5345;
call fdif(zt, yt, d);

call farmalik(lnl, yt, d);
print lnl;

call farmafit(d, ar, ma, sigma, yt);
print d sigma;

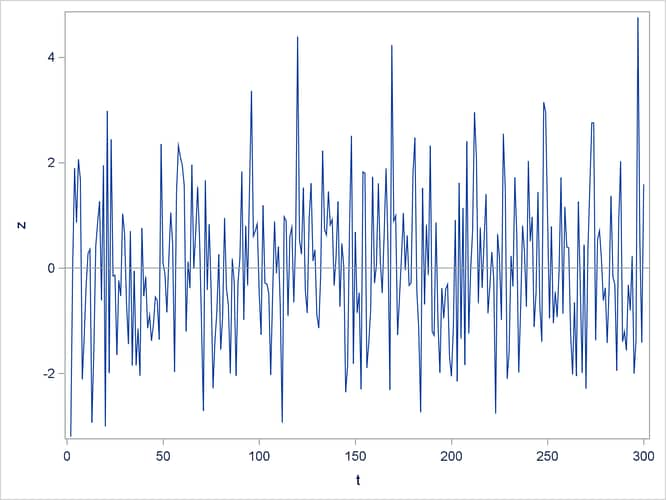
The FARMASIM function generates the data shown in Output 14.14.

Output 14.14: Plot of Generated ARFIMA(0,0.4,0) Process (FARMASIM)

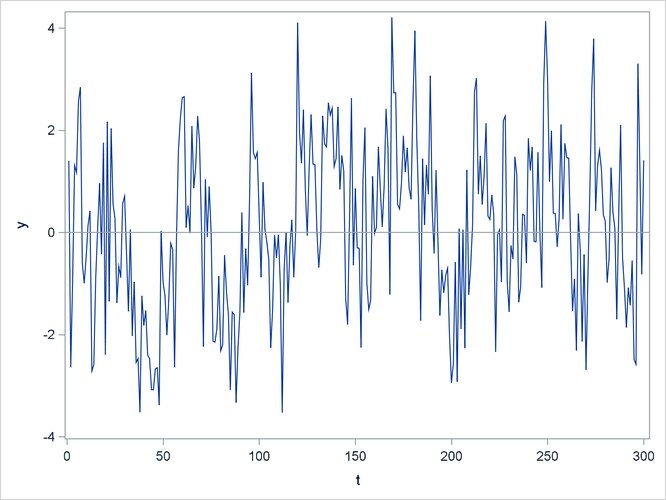
The FDIF function creates the fractionally differenced process. Output 14.15 shows a white noise series.

Output 14.15: Plot of Fractionally Differenced Process (FDIF)

In Output 14.16, the first column displays the autocovariance function of the ARFIMA(0,0.4,0) model, and the second column displays the autocovariance function of the ARFIMA(0,0.05,0) model. The first column decays to zero more slowly than the second column.

Output 14.16: Autocovariance Functions of ARFIMA(0,0.4,0) and ARFIMA(0,0.05,0) Models (FARMACOV)

lag	autocov_D_IS_04	D_IS_005
0	2.0700983	1.0044485
1	1.3800656	0.0528657
2	1.2075574	0.0284662
3	1.1146683	0.0197816
4	1.0527423	0.0152744
5	1.0069709	0.0124972
6	0.9710077	0.0106069
7	0.9415832	0.0092333
8	0.9168047	0.008188
9	0.8954836	0.0073647
10	0.8768277	0.0066985
11	0.8602838	0.006148
12	0.8454513	0.0056849

In Output 14.17, the first row value is the log-likelihood function of the ARFIMA(0,0.4,0) model. Because the default option of the estimates method is the conditional sum of squares, the last two rows of Output 14.17 contain missing values.

Output 14.17: Log-Likelihood Function of ARFIMA(0,0.4,0) Model (FARMALIK)

lnl
-101.0599
.
.

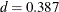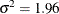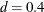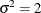Output 14.18 shows parameter estimates for the simulated data. The parameter estimates are $d=0.387$ and $\sigma ^2=1.96$ , whereas the true parameters of the data generating process are $d=0.4$ and $\sigma ^2=2$ .

Output 14.18: Parameter Estimation of ARFIMA(0,0.4,0) Model (FARMAFIT)

d	sigma
0.386507	1.9610507