Sparse Matrix Algorithms

Example: Biconjugate Gradient Algorithm

The biconjugate gradient algorithm is meant for general sparse linear systems. Matrix symmetry is no longer assumed, and a complete list of nonzero coefficients must be provided. Consider the following matrix:

$A = \left(\begin{array}{ccc} 10 & 0 & 0.2 \\ 0.1 & 3 & 0 \\ 0 & 0 & 4 \end{array}\right)$

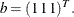
with $b = (1\, 1\, 1)^ T.$

The code for this example is as follows:


   /* biconjugate gradient algorithm */

   /*  value  row column */
   A = { 10    1     1,
         3     2     2,
         4     3     3,
         0.1   2     1,
         0.2   1     3 };

   /* vector of right-hand sides */
   b = {1, 1, 1};

   /* desired solution tolerance */
   tol = 1e-9;

   /* maximum number of iterations */
   maxit = 10000;

   /* allocate history/progress */
   hist = j(50, 1);

   /* initial guess (optional) */
   start = {2, 3, 4};

   /* call biconjugate gradient subroutine */
   call itsolver (
      x, st, it,            /* output parameters */
      'bicg', a, b, 'milu', /* input parameters */
      tol,                  /* optional control parameters */
      maxit,
      start,
      hist);

   /* Print results */
   print  x;
   print st;
   print it;

Here is the output:

It is important to observe the resultant tolerance in order to know how effective the solution is.