Language Reference
TOEPLITZ Function
TOEPLITZ (a);
The TOEPLITZ function generates a Toeplitz matrix from a vector, or a block Toeplitz matrix from a matrix. A block Toeplitz
matrix has the property that all matrices on the diagonals are the same. The argument a is an 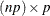 or
or 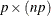 matrix; the value returned is the
matrix; the value returned is the 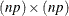 result.
result.
The TOEPLITZ function uses the first 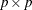 submatrix,
submatrix, 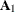 , of the argument matrix as the blocks of the main diagonal. The second
, of the argument matrix as the blocks of the main diagonal. The second 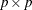 submatrix,
submatrix, 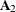 , of the argument matrix forms one secondary diagonal, with the transpose
, of the argument matrix forms one secondary diagonal, with the transpose 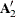 forming the other. The remaining diagonals are formed accordingly. If the first
forming the other. The remaining diagonals are formed accordingly. If the first 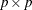 submatrix of the argument matrix is symmetric, the result is also symmetric. If
submatrix of the argument matrix is symmetric, the result is also symmetric. If 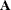 is
is 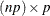 , the first p columns of the returned matrix,
, the first p columns of the returned matrix, 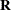 , are the same as
, are the same as 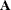 . If
. If 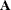 is
is 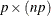 , the first p rows of
, the first p rows of 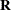 are the same as
are the same as 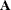 .
.
The TOEPLITZ function is especially useful in time series applications, where the covariance matrix of a set of variables with its lagged set of variables is often assumed to be a block Toeplitz matrix.
If
![\[ \bA = \left[ \bA _1 | \bA _2 | \bA _3 |\cdots | \bA _ n \right] \]](images/imlug_langref1383.png)
and if 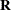 is the matrix formed by the TOEPLITZ function, then
is the matrix formed by the TOEPLITZ function, then
![\[ \bR = \left[ \begin{array}{ccccccccc} \bA _1 & | & \bA _2 & | & \bA _3 & | & \cdots & | & \bA _ n \\ \bA _2^{\prime } & | & \bA _1 & | & \bA _2 & | & \cdots & | & \bA _{n-1} \\ \bA _3^{\prime } & | & \bA _2^{\prime } & | & \bA _1 & | & \cdots & | & \bA _{n-2} \\ \vdots & & & & & & \\ \bA _ n^{\prime } & | & \bA _{n-1}^{\prime } & | & \bA _{n-2}^{\prime } & | & \cdots & | & \bA _1 \end{array} \right] \]](images/imlug_langref1384.png)
If
![\[ \bA = \left[ \begin{array}{c} \bA _1 \\ \bA _2 \\ \vdots \\ \bA _ n \end{array} \right] \]](images/imlug_langref1385.png)
and if 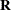 is the matrix formed by the TOEPLITZ function, then
is the matrix formed by the TOEPLITZ function, then
![\[ \bR = \left[ \begin{array}{ccccccccc} \bA _1 & | & \bA _2^{\prime } & | & \bA _3^{\prime } & | & \cdots & | & \bA _ n^{\prime } \\ \bA _2 & | & \bA _1 & | & \bA _2^{\prime } & | & \cdots & | & \bA _{n-1}^{\prime } \\ \vdots & & & & & & \\ \bA _ n & | & \bA _{n-1} & | & \bA _{n-2} & | & \cdots & | & \bA _1 \end{array} \right] ~ \]](images/imlug_langref1386.png)
Three examples follow:
r1 = toeplitz(1:5);
r2 = toeplitz({1 2 ,
3 4 ,
5 6 ,
7 8});
r3 = toeplitz({1 2 3 4,
5 6 7 8});
print r1, r2, r3;
Figure 25.413: Toeplitz Matrices