Language Reference
SOLVELIN Call
CALL SOLVELIN (x, status, A, b, method);
The SOLVELIN subroutine uses direct decomposition to solve sparse symmetric linear systems.
The SOLVELIN subroutine returns the following values:
- x
-
is the solution to
.
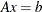- status
-
is the final status of the solution.
The input arguments to the SOLVELIN subroutine are as follows:
- A
-
is the sparse coefficient matrix in the equation
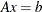. You can use SPARSE function
to convert a matrix from dense to sparse storage.
- b
-
is the right side of the equation
.
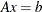- method
-
is the name of the decomposition to be used.
The input matrix A represents the coefficient matrix in sparse format; it is an n by 3 matrix, where n is the number of nonzero elements. The first column contains the nonzero values, while the second and third columns contain the row and column locations for the nonzero elements, respectively. Since A is assumed to be symmetric, only the elements on and below the diagonal should be specified, and it is an error to specify elements above the diagonal.
The solution to the system is returned in x. Your program should also check the returned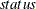 
to make sure that a solution was found.
- status = 0
-
indicates success.
- status = 1
-
indicates the matrix A is not positive-definite.
- status = 2
-
indicates the system ran out of memory.
If the SOLVELIN subroutine is unable to solve your system, you can try the iterative method ITSOLVER subroutine .
Two different factorization methods are available from the call, Cholesky and Symbolic LDL, specified as ’CHOL’ or ’LDL’ with
the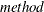 
parameter. Both these factorizations are applicable only to positive-definite symmetric systems; if your system is not positive-definite
or not symmetric, you can use an ITSOLVER call
.
The following example uses SOLVELIN to solve the system:
![\[ \left[ \begin{array}{llll} 3 & 1.1 & 0 & 0 \\ 1.1 & 4 & 1 & 3.2 \\ 0 & 1 & 10 & 0 \\ 0 & 3.2 & 0 & 3 \end{array} \right] x = \left[ \begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array} \right] \]](images/imlug_langref1322.png)
/* value row column */
A = { 3 1 1,
1.1 2 1,
4 2 2,
1 3 2,
3.2 4 2,
10 3 3,
3 4 4};
/* right hand side */
b = {1, 1, 1, 1};
call solvelin(x, status, A, b, 'LDL');
print status x;