Language Reference

ROOT Function

ROOT (matrix <, OnError>);

The ROOT function performs the Cholesky decomposition of a symmetric and positive definite matrix. The arguments are as follows:

matrix: specifies a symmetric and positive definite matrix.
OnError: is an optional string that controls the behavior of the function when matrix is not positive definite. The default behavior is to stop with an error if matrix is not positive definite. If the string has the value "NoError", the function returns a matrix of missing values but does not stop with an error.

The Cholesky decomposition factors the symmetric, positive definite matrix, 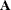$\bA$ , into the product

$\bA = \bU ^{\prime }\bU$

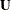where $\bU$ is upper triangular.

For example, the following statements compute the upper-triangular matrix, U, in the Cholesky decomposition of a matrix:

A = {25  0  5,
      0  4  6,
      5  6 59};
U = root(A);
print U;

Figure 25.330: Cholesky Decomposition

U
5	0	1
0	2	3
0	0	7

If you need to solve a linear system and you already have a Cholesky decomposition of your matrix, then use the TRISOLV function as illustrated by the following statements:

b = {5, 2, 53};
/* Want to solve A * v = b.
   First solve U` z = b,
   then solve U v = z */
z = trisolv(2, U, b);
v = trisolv(1, U, z);
print v;

Figure 25.331: Solution to a Linear System

v
0
-1
1

The ROOT function performs most of its computations in the memory allocated for returning the Cholesky decomposition.

You can use the optional argument to test whether a matrix is positive definite, as shown in the following statements:

call randseed(12345);
count = 0;
x = j(3,3);
do i = 1 to 10;
   call randgen(x,"Normal");
   m = x` + x + 2*I(3); /* symmetric, but might not be pos. def. */
   g = root(m, "NoError");
   if all(g=.) then count = count + 1;
end;
msg = char(count) + " out of 10 matrices were not positive definite";
print msg;

Figure 25.332: Test Whether Matrices Are Positive Definite

msg
4 out of 10 matrices were not positive definite