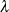Language Reference

RANDGEN Call

Subsections:

Vectors of Parameters
Bernoulli Distribution
Beta Distribution
Binomial Distribution
Cauchy Distribution
Chi-Square Distribution
Erlang Distribution
Exponential Distribution
F Distribution ( $F_{n,d}$ )
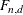Gamma Distribution
Geometric Distribution
Hypergeometric Distribution
Laplace Distribution
Logistic Distribution
Lognormal Distribution
Negative Binomial Distribution
Normal Distribution
Normal Mixture Distribution
Pareto Distribution
Poisson Distribution
t Distribution
Table Distribution
Triangle Distribution
Tweedie Distribution
Uniform Distribution
Wald (Inverse Gaussian) Distribution
Weibull Distribution
Summary of Distributions

CALL RANDGEN (result, distname <, parm1> <, parm2> <, parm3> );

The RANDGEN subroutine generates random numbers from a specified distribution.

The input arguments to the RANDGEN subroutine are as follows:

result: is a matrix that is to be filled with random samples from the specified distribution.
distname: is the name of the distribution.
parm1: is a distribution parameter.
parm2: is a distribution parameter.
parm3: is a distribution parameter.

The RANDGEN subroutine generates random numbers by using the same numerical method as the RAND function in Base SAS software, with the efficiency optimized for matrices. You can initialize the random number stream that is used by RANDGEN by calling the RANDSEED subroutine . The result parameter should be preallocated to a size equal to the number of values that you want to generate. If result is not initialized, then it receives a single random value.

The following statements fill a vector with 1,000 random values from a standard normal distribution:

call randseed(12345);
x = j(1000,1); /* allocate (1000 x 1) vector */
call randgen(x, "Normal"); /* fill it */

Vectors of Parameters

Except for the "Table" and "NormalMix" distributions, the distribution parameters are usually scalar values. However, the RANDGEN subroutine also accepts vectors of parameters. If result is an 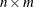$n \times m$ matrix, then parm1, parm2, and parm3 can contain 1, n, m, or 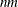$nm$ elements. The different sizes are interpreted as follows:

If the parameters are scalar quantities, each element of result is a sample value from the same distribution.
Otherwise, if the parameters contain m elements, the jth column of the result matrix consists of random values drawn from the distribution with parameters param1[j], param2[j], and param3[j].
Otherwise, if the parameters contain n elements, the ith row of the result matrix consists of random values drawn from the distribution with parameters param1[i], param2[i], and param3[i].
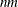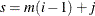Otherwise, if the parameters contain $nm$ elements, the (i, j) element of the result matrix contains a random value drawn from the distribution with parameters param1[s], param2[s], and param3[s], where $s = m(i-1)+j$ .

All parameters must be the same length. You cannot specify a scalar for one parameter and a vector for another. If you pass in parameter vectors that do not satisfy one of the above conditions, then the first element of each parameter is used.

As an example, the jth column of the following matrix is a sample drawn from a normal population with mean j and standard deviation 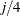$j/4$ :

n = 5; m = 4;
x = j(n,m);
Mu = 1:m;
Sigma = (1:m)/m;
call randgen(x, "Normal", Mu, Sigma);
print x;

Figure 25.303: Columns Drawn from Different Distributions

x
0.7953097	2.109807	2.5903507	4.567692
1.1153841	1.9143935	3.5193908	4.461049
1.1036757	2.6768648	3.3873821	4.5642427
1.1543757	1.6322845	2.6431948	4.2777107
0.8030879	1.4097247	3.0206292	2.6724841

The following sections describe the distributions that are supported.

Bernoulli Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} 1 & \mbox{for } p=0,x=0\\ p^ x(1-p)^{1-x} & \mbox{for } 0<p<1,x=0,1\\ 1 & \mbox{for } p=1,x=1 \end{array} \right.$

The possible values of x are 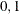${0,1}$ . The parameter p, 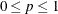$0 \leq p \leq 1$ , is the probability of a "success." A success means that x has the value 1.

Beta Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{ \Gamma (a+b)}{\Gamma (a)\Gamma (b)}x^{a-1}(1-x)^{b-1}$

The range of x is 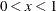$0 < x < 1$ , and a and b are required shape parameters with values 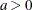$a > 0$ and $b > 0$ .

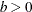Binomial Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} 1 & \mbox{for } p=0,x=0\\ {n \choose x}p^ x(1-p)^{n-x} & \mbox{for } 0<p<1,x=0,\ldots ,n\\ 1 & \mbox{for } p=1,x=1 \end{array} \right.$

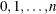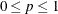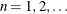The range of x is ${0,1,\ldots ,n}$ . The parameter p is the success probability, with range $0 \leq p \leq 1$ . The parameter n specifies the number of independent trials, $n = 1,2,\ldots$ .

Intuitively, x is the number of successes in n Bernoulli trials with probability p.

Cauchy Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{1}{\pi (1+x^2)}$

The range of x is 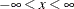$-\infty < x < \infty$ .

Chi-Square Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{2^{-d/2}}{\Gamma (\frac{d}{2})}x^{d/2-1}e^{-x/2}$

The range of x is 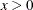$x > 0$ . The parameter d represents degrees of freedom, with $d > 0$ .

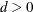Erlang Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{1}{\lambda ^ a \Gamma (a)}x^{a-1}e^{-x/\lambda }$

The Erlang distribution is a gamma distribution with an integer value for the shape parameter, a.

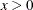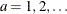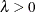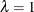The range of x is $x > 0$ . The parameter a is an integer shape parameter, $a = 1,2,\ldots$ . The optional shape parameter $\lambda >0$ has the default value $\lambda =1$ .

Exponential Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{e^{-x/\sigma }}{\sigma }$

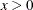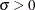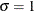The range of x is $x > 0$ . The optional shape parameter $\sigma >0$ has the default value $\sigma =1$ .

F Distribution (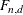 $F_{n,d}$ )

The values of x are drawn from the probability density function:

$f(x) = \frac{\Gamma (\frac{n+d}{2}) n^{\frac{n}{2} } d^{\frac{d}{2}} x^{\frac{n}{2}-1}}{\Gamma (\frac{n}{2})\Gamma (\frac{d}{2})(d+n x)^{\frac{n+d}{2}}}$

The range of x is 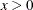$x > 0$ . The two parameters n and d are degrees of freedom, with values 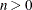$n > 0$ and $d > 0$ .

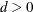Gamma Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{x^{a-1}}{\lambda ^ a \Gamma (a)}e^{-x/\lambda }$

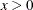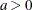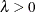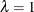The range of x is $x > 0$ . The parameter a is a shape parameter, $a > 0$ . The optional shape parameter $\lambda >0$ has the default value $\lambda =1$ .

Geometric Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} (1-p)^{x-1}p & \mbox{for } 0<p<1,x=1,2,\ldots \\ 1 & \mbox{for } p=1,x=1 \end{array} \right.$

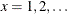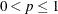The range of x is $x = 1,2,\ldots$ . The parameter p is the success probability, with range $0 < p \leq 1$ .

Intuitively, x is the number of Bernoulli trials (with probability p) until the first success occurs.

Hypergeometric Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{{R \choose x}{{N-R}\choose {k-x}}}{{N \choose k}}$

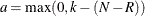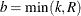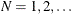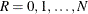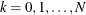The range of x is $[a,b]$ , where $a = \max (0,k-(N-R))$ and $b=\min (k,R)$ . The parameter N is the population size, with range $N = 1,2,\ldots$ . The parameter R is the size of the category of interest, with range $R = 0,1,\ldots ,N$ . The parameter k is the sample size, with range $k = 0,1,\ldots ,N$ .

Intuitively, x is obtained by the following experiment. Put R red balls and 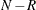$N-R$ black balls into an urn. The value x is the number of red balls in a sample of size k that is drawn from the urn without replacement.

Laplace Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{1}{2\lambda } \exp \left(-\frac{|x-\theta |}{\lambda }\right)$

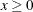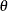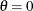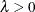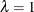The range of x is $x \geq 0$ . The optional location parameter $\theta$ has the default value $\theta =0$ . The optional scale parameter $\lambda > 0$ has the default value $\lambda =1$ .

Logistic Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{\exp \left(-(x-\theta )/\lambda \right)}{\lambda \left(1+\exp \left(-(x-\theta )/\lambda \right) \right)^2}$

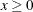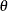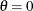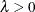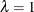The range of x is $x \geq 0$ . The optional location parameter $\theta$ has the default value $\theta =0$ . The optional scale parameter $\lambda > 0$ has the default value $\lambda =1$ .

Lognormal Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{1}{x\lambda \sqrt {2\pi }} \exp \left(-\frac{(\ln (x)-\theta )^2}{2\lambda ^2}\right)$

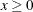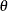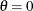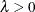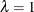The range of x is $x \geq 0$ . The optional log-scale parameter $\theta$ has the default value $\theta =0$ . The optional shape parameter $\lambda > 0$ has the default value $\lambda =1$ .

Negative Binomial Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} {{x+k-1}\choose {k-1}}(1-p)^ xp^ k & \mbox{for } 0<p<1,x=0,1,\ldots \\ 1 & \mbox{for } p=1,x=0 \end{array} \right.$

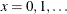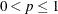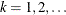The range of x is $x = 0,1,\ldots$ . The parameter p is the success probability with range $0 < p \leq 1$ . The parameter k is an integer that counts the number of successes, with range $k = 1,2,\ldots$ .

Intuitively, x is the number of failures before the kth success during a series of Bernoulli trials with probability of success p.

Normal Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{1}{\lambda \sqrt {2\pi }}\exp \left(-\frac{(x-\theta )^2}{2\lambda ^2}\right)$

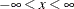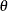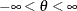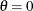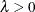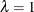The range of x is $-\infty < x < \infty$ . The optional parameter $\theta$ ( $-\infty < \theta < \infty$ ) is the mean (location) parameter, which has the default value $\theta =0$ . The optional parameter $\lambda > 0$ is the standard deviation, with the default value $\lambda =1$ .

Normal Mixture Distribution

The values of x are drawn from the probability density function:

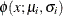$f(x) = \sum _{i=1}^ n p_ i \phi (x; \mu _ i, \sigma _ i)$

where $\phi (x; \mu _ i, \sigma _ i)$ is the normal PDF with mean 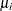$\mu _ i$ and standard deviation 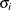$\sigma _ i$ , and where p is a vector of probabilities such that

$\sum _{i=1}^ n p_ i = 1$

The parameters p, 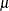$\mu$ , and $\sigma$ are vectors with n elements.

Pareto Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{a}{k} \left( \frac{k}{x} \right)^{a+1}$

The range of x is 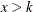$x > k$ . The shape parameter a is valid for 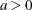$a>0$ . The optional scale parameter 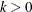$k>0$ has the default value $k=1$ .

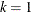Poisson Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{m^ xe^{-m}}{x!}$

The range of x is 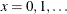$x = 0,1,\ldots$ . The parameter m is a rate parameter with range $m > 0$ .

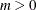t Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{\Gamma \left(\frac{d+1}{2}\right)}{\sqrt {d\pi }\, \Gamma \left(\frac{d}{2}\right)}\left(1+\frac{x^2}{d}\right)^{-\frac{d+1}{2}}$

The range of x is 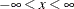$-\infty < x < \infty$ . The parameter d is the degrees of freedom, with the range $d > 0$ .

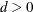Table Distribution

The values of x are drawn from the probability density function:

$f(i) = \left\{ \begin{array}{ll} p_ i & \mbox{for } i = 1,2,\ldots ,n\\ 1-\sum _{j=1}^ np_ j & \mbox{for } i = n+1 \end{array} \right.$

where p is a vector of probabilities, such that 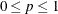$0 \leq p \leq 1$ , and n is the largest integer such that 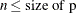$n \leq \mbox{size of p}$ and

$\sum _{j=1}^ n p_ j \leq 1$

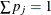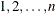Notice that if $\sum p_ j = 1$ , then the values of x are in the range $1,2,\ldots ,n$ .

Triangle Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} \frac{2x}{h} & \mbox{for } 0 \leq x \leq h\\ \frac{2(1-x)}{1-h} & \mbox{for } h < x \leq 1 \end{array} \right.$

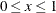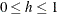The range of x is $0 \leq x \leq 1$ . The parameter h is the horizontal location of the peak of the triangle, with range $0 \leq h \leq 1$ .

Tweedie Distribution

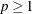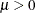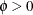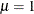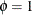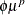Tweedie distributions have three parameters: $p\geq 1$ is the power parameter, $\mu >0$ is the mean of the distribution, and $\phi >0$ is a scale parameter. The default values for the optional parameters are $\mu =1$ and $\phi =1$ . The Tweedie distribution has the property that the variance of the distribution is equal to $\phi \mu ^ p$ .

The range of x is 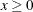$x \geq 0$ . The density function is given by

$f(x) = a(x,\phi ) \exp \left[ \frac{1}{\phi } \left( \frac{x \mu ^{1-p}}{1-p} - \kappa (\mu ,p) \right) \right]$

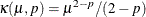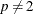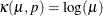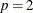where $\kappa (\mu ,p) = \mu ^{2-p}/(2-p)$ for $p \neq 2$ and $\kappa (\mu ,p) = \log (\mu )$ for $p=2$ . The function 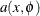$a(x, \phi )$ does not have an analytical expression, but is typically represented by an infinite series.

For most modeling tasks, 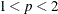$1 < p< 2$ . For p in this range, the Tweedie distribution is a sum of N gamma random variables, where N is Poisson distributed. For details, see the documentation for the SEVERITY procedure in the SAS/ETS User's Guide. The documentation for the PDF function in SAS Language Reference: Dictionary is also relevant.

Uniform Distribution

The values of x are drawn from the probability density function:

$f(x) = \left\{ \begin{array}{ll} 1 & \mbox{if} \; a=b \\ \frac{1}{|b-a|} & \mbox{if} \; a \neq b \end{array} \right.$

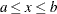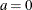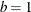The range of x is $a \leq x \leq b$ . The parameters a and b default to the values $a=0$ and $b=1$ . You must specify values for both a and b if you do not want to use the default values.

Wald (Inverse Gaussian) Distribution

The values of x are drawn from the probability density function:

$f(x) = \left(\frac{\lambda }{2\pi x^3}\right)^{\frac{1}{2}} \exp \left(\frac{-\lambda (x-\theta )^2}{2\lambda ^2 x}\right)$

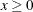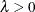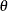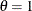The range of x is $x \geq 0$ . The parameter $\lambda > 0$ is a shape parameter. The optional parameter $\theta$ has the default value $\theta =1$ .

Notice that many references, including the MCMC procedure, list 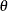$\theta$ as the first parameter for the inverse Gaussian distribution. However, the 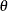$\theta$ parameter is listed last for the RAND, PDF, CDF, and QUANTILE functions because it an optional parameter.

Weibull Distribution

The values of x are drawn from the probability density function:

$f(x) = \frac{a}{b}\left(\frac{x}{b}\right)^{a-1} \exp \left(-\left(\frac{x}{b}\right)^ a\right)$

The range of x is 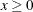$x \geq 0$ . The shape parameters a and b are have values 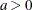$a > 0$ and $b > 0$ .

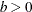Summary of Distributions

Table 25.5 describes how parameters of the RANDGEN call correspond to the distribution parameters.

Table 25.5: Parameter Assignments for Distributions

Distribution	distname	parm1	parm2	parm3
Bernoulli	'BERNOULLI'	p
Beta	'BETA'	a	b
Binomial	'BINOMIAL'	p	n
Cauchy	'CAUCHY'
Chi-Square	'CHISQUARE'	d
Erlang	'ERLANG'	a	< $\lambda =1$ >
Exponential	'EXPONENTIAL'	< $\sigma =1$ >
$F_{n,d}$	'F'	n	d
Gamma	'GAMMA'	a	< $\lambda =1$ >
Geometric	'GEOMETRIC'	p
Hypergeometric	'HYPERGEOMETRIC'	N	R	n
Laplace	'LAPLACE'	< $\theta =0$ >	< $\lambda =1$ >
Logistic	'LOGISTIC'	< $\theta =0$ >	< $\lambda =1$ >
Lognormal	'LOGNORMAL'	< $\theta =0$ >	< $\lambda =1$ >
Negative Binomial	'NEGBINOMIAL'	p	k
Normal	'NORMAL'	< $\theta =0$ >	< $\lambda =1$ >
Normal Mixture	'NORMALMIX'	p	$\mu$	$\sigma$
Pareto	'PARETO'	a	< $k=1$ >
Poisson	'POISSON'	m
t	'T'	d
Table	'TABLE'	p
Triangle	'TRIANGLE'	h
Tweedie	'TWEEDIE'	p	< $\mu =1$ >	< $\phi =1$ >
Uniform	'UNIFORM'	< $a=0$ >	< $b=1$ >
Wald	'WALD' or 'IGAUSS'	$\lambda$	< $\mu =1$ >
Weibull	'WEIBULL'	a	b

The distname argument can be in lowercase or uppercase, and you need to specify only enough letters to distinguish one distribution from the others, as shown by the following statements:

/* generate 10 samples from a Bernoulli distribution */
r = j(10, 1, .);         /* allocate room for samples */
call randgen(r, "ber", 0.5);

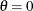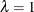Optional arguments are enclosed in angle brackets, along with the default value when the argument is not specified. For example, if you do not supply values for the parameters of the normal distribution, the default values of $\theta =0$ and $\lambda =1$ are used.

The following example illustrates the RANDGEN call for various distributions:

call randseed(12345);
/* get four random observations from each distribution */
x = j(1, 4, .);
/* each row comes from a different distribution */
DiscreteDist = {'BERN','BINOM','GEOM','HYPER',
                'NEGB','POISSON','TABLE'};
D = j(nrow(DiscreteDist), 4, .);
i = 1;
call randgen(x, 'BERN', 0.75);        D[i, ] = x;  i = i+1;
call randgen(x, 'BINOM', 0.75, 10);   D[i, ] = x;  i = i+1;
call randgen(x, 'GEOM', 0.02);        D[i, ] = x;  i = i+1;
call randgen(x, 'HYPER', 10, 3, 5);   D[i, ] = x;  i = i+1;
call randgen(x, 'NEGB', 0.8, 5);      D[i, ] = x;  i = i+1;
call randgen(x, 'POISSON', 6.1);      D[i, ] = x;  i = i+1;
p = {0.2 0.5 0.3};
call randgen(x, 'TABLE', p);          D[i, ] = x;  i = i+1;
print D[rowname=DiscreteDist label="Discrete"];

ContinDist = {'BETA','CAUCHY','CHISQ','ERLANG','EXPO',
              'F','GAMMA','LAPLACE','LOGISTIC','LOGN',
              'NORMAL','NORMALMIX','PARETO','T',
              'TRIANGLE','TWEEDIE','UNIFORM','WALD','WEIB'};
C = j(nrow(ContinDist), 4, .);
i = 1;
call randgen(x, 'BETA', 3, 0.1);      C[i, ] = x;  i = i+1;
call randgen(x, 'CAUCHY');            C[i, ] = x;  i = i+1;
call randgen(x, 'CHISQ', 22);         C[i, ] = x;  i = i+1;
call randgen(x, 'ERLANG',  7);        C[i, ] = x;  i = i+1;
call randgen(x, 'EXPO');              C[i, ] = x;  i = i+1;
call randgen(x, 'F', 12, 322);        C[i, ] = x;  i = i+1;
call randgen(x, 'GAMMA', 7.25);       C[i, ] = x;  i = i+1;
call randgen(x, 'LAPLACE');           C[i, ] = x;  i = i+1;
call randgen(x, 'LOGISTIC');          C[i, ] = x;  i = i+1;
call randgen(x, 'LOGN');              C[i, ] = x;  i = i+1;
call randgen(x, 'NORMAL');            C[i, ] = x;  i = i+1;
p = {0.2 0.5 0.3};  mu = {0 5 10}; sig = {1 1 2};
call randgen(x, 'NORMALMIX',p,mu,sig); C[i,] = x;  i = i+1;
call randgen(x, 'PARETO', 3, 1);      C[i, ] = x;  i = i+1;
call randgen(x, 'T', 4);              C[i, ] = x;  i = i+1;
call randgen(x, 'TRIANGLE', 0.7);     C[i, ] = x;  i = i+1;
call randgen(x, 'TWEEDIE', 1.7);      C[i, ] = x;  i = i+1;
call randgen(x, 'UNIFORM');           C[i, ] = x;  i = i+1;
call randgen(x, 'WALD', 1, 2);        C[i, ] = x;  i = i+1;
call randgen(x, 'WEIB', 0.25, 2.1);   C[i, ] = x;  i = i+1;
print C[rowname=ContinDist label="Continuous"];

Figure 25.304: Random Numbers from Various Distributions

Discrete
BERN	1	0	1	0
BINOM	6	8	7	8
GEOM	22	29	132	4
HYPER	1	2	3	2
NEGB	1	1	1	3
POISSON	10	2	11	5
TABLE	2	2	2	2

Continuous
BETA	0.9698912	0.9986741	0.9530356	0.9999999
CAUCHY	-0.351223	-79.19193	-0.875086	0.2633447
CHISQ	16.501429	10.905074	21.223624	15.693628
ERLANG	3.9509215	3.9110053	12.242025	4.2987446
EXPO	0.1435695	0.6908117	0.2160011	1.41259
F	0.5212328	0.7306928	1.0089965	0.9442868
GAMMA	6.6019823	11.56066	10.237334	2.6774555
LAPLACE	-0.084906	2.9727044	2.7944056	-1.302167
LOGISTIC	0.1334806	-1.613977	-0.528595	-0.418451
LOGN	1.2039346	1.5589409	0.2231522	0.1560639
NORMAL	1.2507254	-0.779791	-1.716859	0.091384
NORMALMIX	1.5133453	3.1300929	4.4290679	5.3063411
PARETO	1.2940105	1.0310942	1.4971162	1.2676456
T	0.2666685	0.2312119	-0.047974	-0.069328
TRIANGLE	0.3098931	0.3216791	0.7828233	0.6975677
TWEEDIE	0.0256424	1.7446859	2.8313134	0.6429287
UNIFORM	0.9101531	0.4957422	0.6919957	0.7501369
WALD	0.3298129	2.4390822	0.3872	1.6025807
WEIB	0.000166	62.455757	17.343105	0.0000656

Language Reference

RANDGEN Call

Vectors of Parameters

Bernoulli Distribution

Beta Distribution

Binomial Distribution

Cauchy Distribution

Chi-Square Distribution

Erlang Distribution

Exponential Distribution

F Distribution ()

Gamma Distribution

Geometric Distribution

Hypergeometric Distribution

Laplace Distribution

Logistic Distribution

Lognormal Distribution

Negative Binomial Distribution

Normal Distribution

Normal Mixture Distribution

Pareto Distribution

Poisson Distribution

t Distribution

Table Distribution

Triangle Distribution

Tweedie Distribution

Uniform Distribution

Wald (Inverse Gaussian) Distribution

Weibull Distribution

Summary of Distributions

F Distribution ( $F_{n,d}$ )