Language Reference
KALDFF Call
CALL KALDFF (pred, vpred, initial, s2, data, lead, int, coef, var, intd, coefd <*>, n0 <*>, at <*>, mt <*>, qt );
The KALDFF subroutine computes the one-step forecast of state vectors in an SSM by using the diffuse Kalman filter. The call
estimates the conditional expectation of  , and also estimates the initial random vector,
, and also estimates the initial random vector, 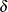 , and its covariance matrix.
, and its covariance matrix.
The input arguments to the KALDFF subroutine are as follows:
- data
-
is a
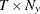 matrix that contains data
matrix that contains data 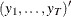 .
.
- lead
-
is the number of steps to forecast after the end of the data set.
- int
-
is an
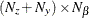 matrix for a time-invariant fixed matrix, or a
matrix for a time-invariant fixed matrix, or a 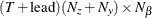 matrix that contains fixed matrices for the time-variant model in the transition equation and the measurement equation—that
is,
matrix that contains fixed matrices for the time-variant model in the transition equation and the measurement equation—that
is, 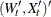 .
.
- coef
-
is an
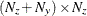 matrix for a time-invariant coefficient, or a
matrix for a time-invariant coefficient, or a 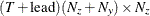 matrix that contains coefficients at each time in the transition equation and the measurement equation—that is,
matrix that contains coefficients at each time in the transition equation and the measurement equation—that is, 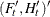 .
.
- var
-
is an
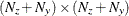 matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation,
or a
matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation,
or a 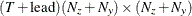 matrix that contains covariance matrices for the error in the transition equation and the error in the measurement equation—that
is,
matrix that contains covariance matrices for the error in the transition equation and the error in the measurement equation—that
is, 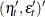 .
.
- intd
-
is an
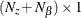 vector that contains the intercept term in the equation for the initial state vector
vector that contains the intercept term in the equation for the initial state vector 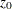 and the mean effect
and the mean effect 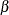 —that is,
—that is, 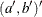 .
.
- coefd
-
is an
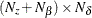 matrix that contains coefficients for the initial state
matrix that contains coefficients for the initial state 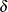 in the equation for the initial state vector
in the equation for the initial state vector 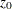 and the mean effect
and the mean effect 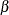 —that is,
—that is, 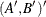 .
.
- n0
-
is an optional scalar including an initial denominator. If n0
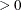 , the denominator for
, the denominator for 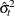 is n0 plus the number
is n0 plus the number 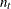 of elements of
of elements of 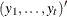 . If n0
. If n0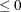 or n0 is not specified, the denominator for
or n0 is not specified, the denominator for 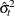 is
is 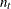 . With n0
. With n0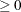 , the initial values,
, the initial values, 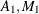 , and
, and 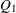 , are assumed to be known and, hence, at, mt, and qt are used for input that contains the initial values. If the value of n0 is negative or n0 is not specified, the initial values for at, mt, and qt are computed. The value of n0 is updated as
, are assumed to be known and, hence, at, mt, and qt are used for input that contains the initial values. If the value of n0 is negative or n0 is not specified, the initial values for at, mt, and qt are computed. The value of n0 is updated as 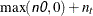 after the KALDFF call.
after the KALDFF call.
- at
-
is an optional
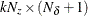 matrix. If n0
matrix. If n0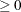 , at contains
, at contains 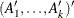 . However, only the first matrix
. However, only the first matrix 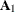 is used as input. When you specify the KALDFF call, at returns
is used as input. When you specify the KALDFF call, at returns 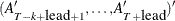 . If n0 is negative or the matrix
. If n0 is negative or the matrix 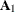 contains missing values,
contains missing values, 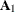 is automatically computed.
is automatically computed.
- mt
-
is an optional
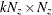 matrix. If n0
matrix. If n0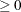 , mt contains
, mt contains 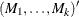 . However, only the first matrix
. However, only the first matrix 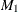 is used as input. If n0 is negative or the matrix
is used as input. If n0 is negative or the matrix 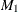 contains missing values, mt is used for output, and it contains
contains missing values, mt is used for output, and it contains 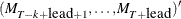 . Note that the matrix
. Note that the matrix 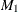 can be used as an input matrix if either of the off-diagonal elements is not missing. The missing element
can be used as an input matrix if either of the off-diagonal elements is not missing. The missing element 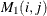 is replaced by the nonmissing element
is replaced by the nonmissing element 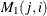 .
.
- qt
-
is an optional
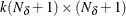 matrix. If n0
matrix. If n0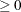 , qt contains
, qt contains 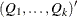 . However, only the first matrix
. However, only the first matrix 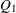 is used as input. If n0 is negative or the matrix
is used as input. If n0 is negative or the matrix 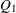 contains missing values, qt is used for output and contains
contains missing values, qt is used for output and contains 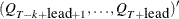 . The matrix
. The matrix 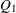 can also be used as an input matrix if either of the off-diagonal elements is not missing since the missing element
can also be used as an input matrix if either of the off-diagonal elements is not missing since the missing element 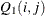 is replaced by the nonmissing element
is replaced by the nonmissing element 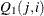 .
.
The KALDFF call returns the following values:
- pred
-
is a
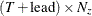 matrix that contains estimated predicted state vectors
matrix that contains estimated predicted state vectors 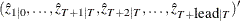 .
.
- vpred
-
is a
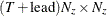 matrix that contains estimated mean square errors of predicted state vectors
matrix that contains estimated mean square errors of predicted state vectors 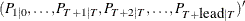 .
.
- initial
-
is an
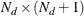 matrix that contains an estimate and its variance for initial state
matrix that contains an estimate and its variance for initial state 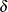 , that is,
, that is, 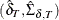 .
.
- s2
-
is a scalar that contains the estimated variance
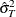 .
.
The KALDFF call computes the one-step forecast of state vectors in an SSM by using the diffuse Kalman filter. The SSM for the diffuse Kalman filter is written
![\begin{eqnarray*} y_ t & = & X_ t \beta + H_ t z_ t + \epsilon _ t \\[0.05in] z_{t+1} & = & W_ t \beta + F_ t z_ t + \eta _ t \\[0.05in] z_0 & = & a + A \delta \\[0.05in] \beta & = & b + B \delta \end{eqnarray*}](images/imlug_langref0623.png)
where  is an
is an 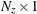 state vector,
state vector, 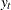 is an
is an 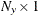 observed vector, and
observed vector, and
![\begin{eqnarray*} \left[ \begin{array}{c} \eta _ t \\ \epsilon _ t \end{array} \right] & \sim & N \left(\mb{0}, \sigma ^2 \left[ \begin{array}{cc} V_ t & G_ t \\ G^{\prime }_ t & R_ t \end{array} \right] \right) \\ \delta & \sim & N(\mu , \sigma ^2\Sigma ) \end{eqnarray*}](images/imlug_langref0624.png)
It is assumed that the noise vector 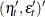 is independent and
is independent and 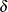 is independent of the vector
is independent of the vector 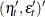 . The matrices,
. The matrices, 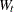 ,
, 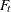 ,
, 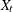 ,
, 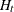 , a, A, b, B,
, a, A, b, B, 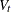 ,
, 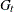 , and
, and 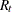 , are assumed to be known. The KALDFF call estimates the conditional expectation of the state vector
, are assumed to be known. The KALDFF call estimates the conditional expectation of the state vector  given the observations. The KALDFF subroutine also produces the estimates of the initial random vector
given the observations. The KALDFF subroutine also produces the estimates of the initial random vector 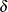 and its covariance matrix. For k-step forecasting where
and its covariance matrix. For k-step forecasting where 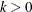 , the estimated conditional expectation at time
, the estimated conditional expectation at time 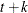 is computed with observations given up to time t. The estimated k-step forecast and its estimated MSE are denoted
is computed with observations given up to time t. The estimated k-step forecast and its estimated MSE are denoted 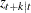 and
and 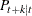 (for
(for 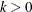 ).
). 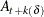 and
and 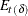 are last-column-deleted submatrices of
are last-column-deleted submatrices of 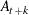 and
and 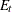 , respectively. The algorithm for one-step prediction is given as follows:
, respectively. The algorithm for one-step prediction is given as follows:
![\begin{eqnarray*} E_ t & = & (X_ t B, ~ y_ t - X_ t b) - H_ t A_ t \\[0.05in] D_ t & = & H_ t M_ t H^{\prime }_ t + R_ t \\[0.05in] Q_{t+1} & = & Q_ t + E^{\prime }_ t D_ t^- E_ t \\[0.05in]& = & \left[\begin{array}{cc} S_ t & s_ t \\ s^{\prime }_ t & q_ t \end{array} \right] \\[0.05in] \hat{\sigma }^2_ t & = & (q_ t - s^{\prime }_ t S_ t^- s_ t)/n_ t \\[0.05in] \hat{\delta }_ t & = & S^-_ t s_ t \\[0.05in] \hat{\Sigma }_{\delta ,t} & = & \hat{\sigma }^2_ t S^-_ t \\[0.05in] K_ t & = & (F_ t M_ t H^{\prime }_ t + G_ t)D^-_ t \\[0.05in] A_{t+1} & = & W_ t(-B, b) + F_ t A_ t + K_ tE_ t \\[0.05in] M_{t+1} & = & (F_ t - K_ t H_ t) M_ t F^{\prime }_ t + V_ t - K_ t G^{\prime }_ t \\[0.05in] z_{t+1|t} & = & A_{t+1}(-\hat{\delta }^{\prime }_ t, 1)^{\prime } \\[0.05in] P_{t+1|t} & = & \hat{\sigma }^2_ t \bM _{t+1} + A_{t+1(\delta )} \hat{\Sigma }_{\delta ,t} A^{\prime }_{t+1(\delta )} \end{eqnarray*}](images/imlug_langref0633.png)
where 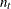 is the number of elements of
is the number of elements of 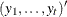 plus
plus 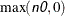 . Unless initial values are given and n0
. Unless initial values are given and n0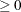 , initial values are set as follows:
, initial values are set as follows:
![\begin{eqnarray*} A_1 & = & W_1(-B,b) + F_1(-A,a) \\[0.05in] M_1 & = & V_1 \\[0.05in] Q_1 & = & \mb{0} \end{eqnarray*}](images/imlug_langref0636.png)
For k-step forecasting where 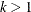 ,
,
![\begin{eqnarray*} A_{t+k} & = & W_{t+k-1}(-B,b) + F_{t+k-1} A_{t+k-1} \\[0.05in] M_{t+k} & = & F_{t+k-1} M_{t+k-1} F^{\prime }_{t+k-1} + V_{t+k-1} \\[0.05in] D_{t+k} & = & H_{t+k} M_{t+k} H^{\prime }_{t+k} + R_{t+k} \\[0.05in] z_{t+k|t} & = & A_{t+k}(-\hat{\delta }^{\prime }_ t,1)^{\prime } \\[0.05in] P_{t+k|t} & = & \hat{\sigma }^2_ t M_{t+k} + A_{t+k(\delta )} \hat{\Sigma }_{\delta ,t} A^{\prime }_{t+k(\delta )} \end{eqnarray*}](images/imlug_langref0637.png)
If there is a missing observation, the KALDFF call computes the one-step forecast for the observation that follows the missing observation as the two-step forecast from the previous observation.
An example that uses the KALDFF call is in the documentation for the KALDFS call .