Language Reference
INVUPDT Function
INVUPDT (matrix, vector<, scalar>);
The INVUPDT function updates a matrix inverse.
The arguments to the INVUPDT function are as follows:
- matrix
-
is an
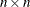 nonsingular matrix. In most applications matrix is symmetric positive definite.
nonsingular matrix. In most applications matrix is symmetric positive definite.
- vector
-
is an
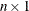 or
or 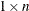 vector.
vector.
- scalar
-
is a numeric scalar.
The Sherman-Morrison-Woodbury formula is
![\[ (\bA + \bU \bV ^{\prime })^{-1} = \bA ^{-1} - \bA ^{-1} \bU (\bI + \bV ^{\prime }\bA ^{-1}\bU )^{-1} \bV ^{\prime }\bA ^{-1} \]](images/imlug_langref0467.png)
where 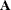 is an
is an 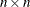 nonsingular matrix and
nonsingular matrix and 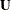 and
and 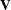 are
are 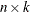 . The formula shows that a rank k update to
. The formula shows that a rank k update to 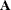 corresponds to a rank k update of
corresponds to a rank k update of 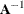 .
.
The INVUPDT function implements the Sherman-Morrison-Woodbury formula for rank-one updates with 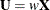 and
and 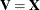 , where
, where 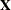 is an
is an 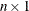 vector and w is a scalar.
vector and w is a scalar.
If 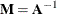 , then you can call the INVUPDT function as follows:
, then you can call the INVUPDT function as follows:
R = invupdt(M, X, w);
This statement computes the following matrix:
![\[ \bR = \bM - w\mb{MX} (\bI + w\bX ^{\prime }\mb{MX})^{-1} \bX ^{\prime }\bM \]](images/imlug_langref0474.png)
The matrix 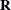 is equivalent to
is equivalent to 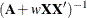 . If
. If 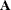 is symmetric positive definite, then so is
is symmetric positive definite, then so is 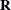 .
.
If w is not specified, then it is given a default value of 1.
A common use of the INVUPDT function is in linear regression. If 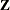 is a design matrix,
is a design matrix, 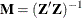 is the associated inverse crossproduct matrix, and
is the associated inverse crossproduct matrix, and  is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that
includes the new observation can be updated from
is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that
includes the new observation can be updated from 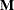 by using the following statement:
by using the following statement:
M2 = invupdt(M, v);
If w is 1, the function adds an observation to the inverse; if w is 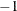 , the function removes an observation from the inverse. If weighting is used, w is the weight.
, the function removes an observation from the inverse. If weighting is used, w is the weight.
To perform the computation, the INVUPDT function uses about 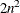 multiplications and additions, where n is the row dimension of the positive definite argument matrix.
multiplications and additions, where n is the row dimension of the positive definite argument matrix.
The following program demonstrates adding or removing observations from a linear fit and updating the inverse crossproduct matrix:
X = {0, 1, 1, 1, 2, 2, 3, 4, 4};
Y = {1, 1, 2, 6, 2, 3, 3, 3, 4};
/* find linear fit */
Z = j(nrow(X), 1, 1) || X; /* design matrix */
M = inv(Z`*Z);
b = M*Z`*Y; /* LS estimate */
resid = Y - Z*b; /* residuals */
print "Original Fit", b resid;
/* residual for observation (1,6) seems too large.
Take obs number 4 out of data set and refit. */
v = z[4,];
M = invupdt(M, v, -1); /* update inverse crossprod */
keepObs = (1:3) || (5:nrow(X));
Z = Z[keepObs, ];
Y = Y[keepObs, ];
b = M*Z`*Y; /* new LS estimate */
print "After deleting observation 4", b;
/* Add a new obs (x,y) = (0,2) and refit. */
obs = {0 2};
v = 1 || obs[1]; /* new row in design matrix */
M = invupdt(M, v);
Z = Z // v;
Y = Y // obs[2];
b = M*Z`*Y; /* new LS estimate */
print "After adding observation (0,2)", b;
Figure 25.171: Refitting Linear Regression Models