Language Reference

HADAMARD Function

HADAMARD (n, <, i> );

The HADAMARD function returns a Hadamard matrix. The arguments to the HADAMARD function are as follows:

n

specifies the order of the Hadamard matrix. You can specify that n is 1, 2, or a multiple of 4. Furthermore, n must satisfy at least one of the following conditions:

  • n 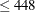$\le 448$ or n equals 596, 604, 612, 732, or 756

  • n – 1 is prime

  • (n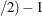$/ 2) - 1$ is prime and n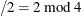$/ 2 = 2\; \mr{mod}\; 4$

  • n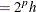$ = 2^ p h$ for some positives integers p and h, and h satisfies one of the preceding conditions

When any other n is specified, the HADAMARD function returns a zero.

i

specifies the row number to return. When i is not specified or i is negative, the full Hadamard matrix is returned.

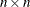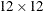The HADAMARD function returns a Hadamard matrix, which is an $n \times n$ matrix that consists entirely of the values 1 and –1. The columns of a Hadamard matrix are all orthogonal. Hadamard matrices are frequently used to make orthogonal array experimental designs for two-level factors. For example, the following statements create a $12 \times 12$ Hadamard matrix: 

h = hadamard(12);
print h[format=2.];

The output is shown in Figure 25.152. The first column is an intercept and the next 11 columns form an orthogonal array experimental design for 11 two-level factors in 12 runs, 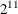$2^{11}$.

Figure 25.152: A Hadamard Matrix

h
1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
1 1 -1 1 -1 -1 -1 1 1 1 -1 1
1 1 1 -1 1 -1 -1 -1 1 1 1 -1
1 -1 1 1 -1 1 -1 -1 -1 1 1 1
1 1 -1 1 1 -1 1 -1 -1 -1 1 1
1 1 1 -1 1 1 -1 1 -1 -1 -1 1
1 1 1 1 -1 1 1 -1 1 -1 -1 -1
1 -1 1 1 1 -1 1 1 -1 1 -1 -1
1 -1 -1 1 1 1 -1 1 1 -1 1 -1
1 -1 -1 -1 1 1 1 -1 1 1 -1 1
1 1 -1 -1 -1 1 1 1 -1 1 1 -1
1 -1 1 -1 -1 -1 1 1 1 -1 1 1 




            

            


            
To request the seventeenth row of a Hadamard matrix of order 448, use the following statement: 


h17 = hadamard(448, 17);