Language Reference
GASETCRO Call
CALL GASETCRO (id, crossprob, type <, parm> );
The GASETCRO subroutine sets the crossover operator for a genetic algorithm optimization. The input arguments to the GASETCRO call are as follows:
- id
-
is the identifier for the genetic algorithm optimization problem, which was returned by the GASETUP function .
- crossprob
-
is the crossover probability, which has a range from zero to one. It specifies the probability that selected members of the current generation undergo crossover to produce new offspring for the next generation.
- type
-
specifies the kind of crossover operator to be used. type is used in conjunction with parm to specify either a user-written module for the crossover operator or one of several other operators, as explained in the following list.
- parm
-
is a matrix whose interpretation depends on the value of type, as described in the following list.
The following list specifies the valid values of the type parameter and the corresponding crossover operators:
- –1
-
specifies that no crossover operator be applied and the new population be generated by applying the mutation operator to the old population, according to the mutation probability.
- 0
-
specifies that a user-written module, whose name is passed in the parm parameter, be used as the crossover operator. This module should be a subroutine with four parameters. The module should return the new offspring solutions in the first two parameters based on the input parent solutions, which are selected by the genetic algorithm and passed into the module in the last two parameters. The module is called once for each crossover operation within the GAREGEN call to create a new generation of solutions.
- 1
-
specifies the simple operator, defined for fixed-length integer and real vector encoding. To apply this operator, a position k within the vector of length n is chosen at random, such that
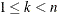 . Then for parents
. Then for parents p1andp2the offspring are as follows:c1= p1[1,1:k] || p2[1,k+1:n]; c2= p2[1,1:k] || p1[1,k+1:n];
For real fixed-length vector encoding, you can specify an additional parameter, a, with the parm parameter, where a is a scalar and
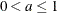 . It modifies the offspring as follows:
. It modifies the offspring as follows:
x2 = a * p2 + (1-a) * p1; c1 = p1[1,1:k] || x2[1,k+1:n]; x1 = a * p1 + (1-a) * p2 c2 = p2[1,1:k] || x1[1,k+1:n];
Note that for a = 1, which is the default value,
x2andx1are the same asp2andp1. Small values of a reduce the difference between the offspring and parents. For integer encoding, the parm parameter is ignored and a is always 1. - 2
-
specifies the two-point operator, defined for fixed-length integer and real vector encoding with length
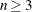 . To apply this operator, two positions
. To apply this operator, two positions 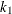 and
and 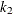 within the vector are chosen at random, such that
within the vector are chosen at random, such that 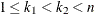 . Element values between those positions are swapped between parents. For parents
. Element values between those positions are swapped between parents. For parents p1andp2the offspring are as follows:c1 = p1[1,1:k1] || p2[1,k1+1:k2] || p1[1,k2+1:n]; c2 = p2[1,1:k1] || p1[1,k1+1:k2] || p2[1,k2+1:n];
For real vector encoding, you can specify an additional parameter, a, in the parm field, where
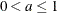 . It modifies the offspring as follows:
. It modifies the offspring as follows:
x2 = a * p2 + (1-a) * p1; c1 = p1[1,1:k1] || x2[1,k1+1:k2] || p1[1,k2+1:n]; x1 = a * p1 + (1-a) * p2; c2 = p2[1,1:k1] || x1[1,k1+1:k2] || p2[1,k2+1:n];
Note that for a = 1, which is the default value,
x2andx1are the same asp2andp1. Small values of a reduce the difference between the offspring and parents. For integer encoding, the parm parameter is ignored if present and a is always 1. - 3
-
specifies the arithmetic operator, defined for real and integer fixed-length vector encoding. This operator computes offspring of parents
p1andp2as follows:c1 = a * p1 + (1-a) * p2; c2 = a * p2 + (1-a) * p1;
where a is a random number between 0 and 1. For integer encoding, each component is rounded off to the nearest integer. An advantage of this operator is that it always produces feasible offspring for a convex solution space. A disadvantage is that it tends to produce offspring toward the interior of the search region, so that it can be less effective if the optimum lies on or near the search region boundary.
- 4
-
specifies the heuristic operator, defined for real fixed-length vector encoding. This operator computes the first offspring from the two parents
p1andp2as follows:c1 = a * (p2 - p1) + p2;
where
p2is the parent with the better objective value and a is a random number between 0 and 1. The second offspring is computed as in the arithmetic operator, as follows:c2 = (1 - a) * p1 + a * p2;
This operator is unusual in that it uses the objective value. It has the advantage of directing the search in a promising direction and automatically fine-tuning the search in an area where solutions are clustered. If upper and lower bound constraints are specified in the GAINIT call , the offspring are checked against the bounds and any component outside its bound is set equal to that bound.
- 5
-
specifies the partial match operator, defined for sequence encoding. This operator produces offspring by transferring a subsequence from one parent and filling the remaining positions in a way consistent with the position and ordering in the other parent. Start with two parents and randomly chosen cut-points as follows:
p1 = {1 2|3 4 5 6|7 8 9}; p2 = {8 7|9 3 4 1|2 5 6};The first step is to cross the selected segments; a missing value (.) indicates a position that is not determined):
c1 = {. . 9 3 4 1 . . .}; c2 = {. . 3 4 5 6 . . .};Next, define a mapping according to the two selected segments, as follows:
![\[ 9\leftrightarrow 3, 3\leftrightarrow 4, 4\leftrightarrow 5, 1\leftrightarrow 6 \]](images/imlug_langref0380.png)
Next, fill in the positions where there is no conflict from the corresponding parent:
c1 = {. 2 9 3 4 1 7 8 .}; c2 = {8 7 3 4 5 6 2 . .};Last, fill in the remaining positions from the subsequence mapping. In this case, for the first child
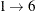 and
and 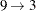 , and for the second child
, and for the second child 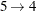 ,
, 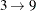 , and
, and 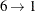 :
:
c1 = {6 2 9 3 4 1 7 8 5}; c2 = {8 7 3 4 5 6 2 9 1};This operator tends to maintain similarity of both the absolute position and relative ordering of the sequence elements, and is useful for a wide range of sequencing problems.
- 6
-
specifies the order operator, defined for sequence encoding. This operator produces offspring by transferring a subsequence of random length and position from one parent and filling the remaining positions according to the order from the other parent. For parents
p1andp2, first choose a subsequence, as follows:p1 = {1 2|3 4 5 6|7 8 9}; p2 = {8 7|9 3 4 1|2 5 6}; c1 = {. . 3 4 5 6 . . .}; c2 = {. . 9 3 4 1 . . .};Starting at the second cut-point, the elements of
p2are in the following order (cycling back to the beginning):2 5 6 8 7 9 3 4 1
After removing 3, 4, 5, and 6, which have already been placed in
c1, you have the following:2 8 7 9 1
Placing these back in order, starting at the second cut-point, yields the following:
c1 = {9 1 3 4 5 6 2 8 7};Applying this logic to
c2yields the following:c2 = {5 6 9 3 4 1 7 8 2};This operator maintains the similarity of the relative order (also called the adjacency) of the sequence elements of the parents. It is especially effective for circular path-oriented optimizations, such as the traveling salesman problem.
- 7
-
specifies the cycle operator, defined for sequence encoding. This operator produces offspring such that the position of each element value in the offspring comes from one of the parents. For example, consider the following parents
p1andp2:p1 = {1 2 3 4 5 6 7 8 9}; p2 = {8 7 9 3 4 1 2 5 6};For the first child, pick the first element from the first parent, as follows:
c1 = {1 . . . . . . . .};To maintain the condition that the position of each element value must come from one of the parents, the position of the '8' value must come from
p1, because the '8' position inp2is already taken by the '1' inc1:c1 = {1 . . . . . . 8 .};Now the position of '5' must come from
p1and so on until the process returns to the first position:c1 = {1 . 3 4 5 6 . 8 9};At this point, choose the remaining element positions from
p2:c1 = {1 7 3 4 5 6 2 8 9};For the second child, starting with the first element from the second parent, similar logic produces the following:
c2 = {8 2 9 3 4 1 7 5 6};This operator is most useful when the absolute position of the elements is of most importance to the objective value.
A GASETCRO call is required when 0 is specified for the encoding parameter in the GASETUP function . But for fixed-length vector and sequence encoding, a default crossover operator is used in the GAREGEN call when no GASETCRO call is made. For sequence encoding, the default is the partial match operator, unless the traveling salesman option was specified in the GASETOBJ call , in which case the order operator is the default. For integer fixed-length vector encoding, the default is the simple operator. For real fixed-length vector encoding, the default is the heuristic operator.
See the GASETUP function for an example.