Language Reference

COVLAG Function

COVLAG (x, k);

The COVLAG function computes a sequence of lagged crossproduct matrices. This function is useful for computing sample autocovariance sequences for scalar or vector time series.

The arguments to the COVLAG function are as follows:

x

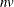is an $n \times nv$ matrix of time series values; n is the number of observations, and $nv$ is the dimension of the random vector.

k

is a scalar, the absolute value of which specifies the number of lags desired. If k is positive, a mean correction is made. If k is negative, no mean correction is made.

The value returned by the COVLAG function is an 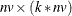$nv \times (k*nv)$ matrix. The ith $nv \times nv$ block of the matrix is the sum

\[ \frac{1}{n} \sum _{j=i}^ n x_ j^{\prime } x_{j-i+1} ~ ~ ~ \mbox{if } k<0 \]

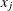where $x_ j$ is the jth row of x. If k > 0, then the ith $nv \times nv$ block of the matrix is

\[ \frac{1}{n} \sum _{j=i}^ n (x_ j-\bar{x})^{\prime }(x_{j-i+1}-\bar{x}) \]

where $\bar{x}$ is a row vector of the column means of x.

For example, the following statements produce a lagged crossproduct matrix: 

x = T(do(-9, 9, 2));
cov = covlag(x, 4);
print cov;

Figure 25.87: Lagged Crossproduct Matrix

cov
33 23.1 13.6 4.9