Language Reference
CONVEXIT Function
CONVEXIT (times, flows, ytm);
The CONVEXIT function computes and returns a scalar that contains the convexity of a noncontingent cash flow. The arguments to the CONVEXIT function are as follows:
- times
-
is an n-dimensional column vector of times. Elements should be nonnegative.
- flows
-
is an n-dimensional column vector of cash flows.
- ytm
-
is the per-period yield-to-maturity of the cash-flow stream. This is a scalar and should be positive.
Convexity is essentially a measure of how duration, the sensitivity of price to yield, changes as interest rates change:
![\[ C = \frac{1}{P} \frac{ d^2 P}{ dy^2 } \]](images/imlug_langref0197.png)
Under certain assumptions, the convexity of cash flows that are not yield-sensitive is given by
![\[ C= \frac{ \sum _{k=1}^{K} t_ k (t_ k+1) \frac{ c(k) }{ (1+y)^{t_ k} } }{ P (1+y)^2 } \]](images/imlug_langref0198.png)
where P is the present value, y is the effective per-period yield-to-maturity, K is the number of cash flows, and the kth cash flow is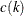 
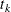periods from the present.
The following statements compute the convexity of a noncontingent cash flow.
timesn = T(do(1, 100, 1)); flows = repeat(10, 100); ytm = 0.1; convexit = convexit(timesn, flows, ytm); print convexit;