Language Reference

BTRAN Function

BTRAN (x, n, m);

The BTRAN function computes the block transpose of a partitioned matrix. The arguments to the BTRAN function are as follows:

x: is an 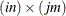$(in) \times (jm)$ numeric matrix.
n: is a scalar with a value that specifies the row dimension of the submatrix blocks.
m: is a scalar with a value that specifies the column dimension of the submatrix blocks.

The argument x is a partitioned matrix formed from submatrices of dimension 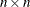$n \times n$ . If the ith, jth submatrix of the argument x is denoted 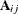$\bA _{ij}$ , then the ith, jth submatrix of the result is $\bA _{ji}$ .

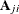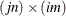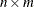The value returned by the BTRAN function is a $(jn) \times (im)$ matrix, the block transpose of x, where the blocks are $n \times m$ .

For example, the following statements compute the block transpose of a matrix:

a11 = {1 1,                   /* a 3 x 2 matrix */
       1 1,
       1 1};
a12 = 1 + a11;
a13 = 2 + a11;
a21 = 3 + a11;
a22 = 4 + a11;
a23 = 5 + a11;

x = (a11 || a12 || a13) //    /* a partitioned matrix  */
    (a21 || a22 || a23);      /* each submatrix is a 3 x 2 block */

z = btran(x, 3, 2);           /* transpose the blocks */
print z;

Figure 25.63: Block Transpose of a Partitioned Matrix

z
1	1	4	4
1	1	4	4
1	1	4	4
2	2	5	5
2	2	5	5
2	2	5	5
3	3	6	6
3	3	6	6
3	3	6	6