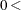Genetic Algorithms
Setting Up the IML Program
After you formulate the GA optimization problem as described in the previous section, executing the genetic algorithm in IML is simple and straightforward. Remember that the current GA implementation in IML is experimental, and will be furthur developed and tested in later SAS releases. The following table summarizes the IML GA modules used to set each of the optimization parameters. IML will use reasonable default values for some of the parameters if they are not specified by the GA calls, and these default values are also listed. Parameters shown in italics are not required in all cases.
Table 22.2: Establishing Optimization Parameters
|
Type |
Set By |
Parameter |
Value |
|---|---|---|---|
|
encoding |
GASETUP |
encoding |
|
|
|
|||
|
|
|||
|
|
|||
|
size |
fixed-length size |
||
|
seed |
initial random seed |
||
|
objective |
GASETOBJ |
id |
returned from GASETUP |
|
objtype |
|
||
|
|
|||
|
|
|||
|
parm |
if objtype=0 or 1, user module |
||
|
if objtype=2, cost coefficients |
|||
|
selection |
GASETSEL |
id |
returned from GASETUP |
|
elite |
integer in [0, population size] |
||
|
type |
|
||
|
|
|||
|
parm |
if type = 0, tournament size |
||
|
if type = 1, real number in [0.5,1] |
|||
|
default if |
elite |
1 |
|
|
not set |
type |
conventional tournament |
|
|
parm |
2 |
||
|
crossover |
GASETCRO |
id |
returned from GASETUP |
|
crossprob |
crossover probability |
||
|
type |
|
||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
parm |
module name for type = 0 |
||
|
|
|||
|
default if |
crossprob |
1.0 |
|
|
not set |
type |
heuristic if encoding=1 |
|
|
simple if encoding=2 |
|||
|
pmatch if encoding=3, objtype 0 |
|||
|
order if objtype=2 (TSP) |
|||
|
mutation |
GASETMUT |
id |
returned from GASETUP |
|
mutprob |
mutation probability |
||
|
type |
|
||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
parm |
delta value if type=2 |
||
|
number of swaps if type=3 |
|||
|
default if |
mutprob |
0.05 |
|
|
not set |
type |
uniform if encoding=1 or 2, bounded |
|
|
delta if encoding=1 or 2, no bounds |
|||
|
swap if encoding=3, not TSP |
|||
|
invert if objtype=1 (TSP) |
After setting the optimization parameters, you are ready to execute the GA. First, an initial solution population must be generated with a GAINIT call. GAINIT implements the initialization phase of the GA, generating an initial population of solutions and evaluating the objective value of each member solution. In the GAINIT call you specify the population size and any constant bounds on the solution domain. Next comes an IML loop that contains a GAREGEN call. GAREGEN implements the regeneration phase of the GA, which generates a new solution population based on selection, crossover, and mutation of the current solution population, then replaces the current population with the new population and computes the new objective function values.
After the GAREGEN call, you can monitor the convergence of the GA by retrieving the objective function values for the current population with the GAGETVAL call. You might check the average value of the objective population, or check only the best value. If the elite parameter is 1 or more, then it is easy to check the best member of the population, since it will always be the first member retrieved.
After your stopping criteria have been reached, you can retrieve the members of the solution population with the GAGETMEM call. To end the optimization, you should always use the GAEND call to free up memory resources allocated to the GA.
Below are some example programs to illustrate setting up and executing a genetic algorithm. The first example illustrates a simple program, a 10-city TSP using all IML defaults. The cost coefficients correspond to the cities being laid out on a two-by-five grid. The optimal route has a total distance of 10.
proc iml;
/* cost coefficients for TSP problem */
coeffs = { 0 1 2 3 4 5 4 3 2 1,
1 0 1 2 3 4 5 4 3 2,
2 1 0 1 2 3 4 5 4 3,
3 2 1 0 1 2 3 4 5 4,
4 3 2 1 0 1 2 3 4 5,
5 4 3 2 1 0 1 2 3 4,
4 5 4 3 2 1 0 1 2 3,
3 4 5 4 3 2 1 0 1 2,
2 3 4 5 4 3 2 1 0 1,
1 2 3 4 5 4 3 2 1 0 };
/* problem setup */
id = gasetup(3, /* 3 -> integer sequence encoding */
10, /* number of locations */
1234 /* initial seed */
);
/* set objective function */
call gasetobj(id,
2, /* 2 -> Traveling Salesman Problem */
coeffs /* cost coefficient matrix */
);
/* initialization phase */
call gainit(id,
100 /* initial population size */
);
/* execute regeneration loop */
niter = 20; /* number of iterations */
bestValue = j(niter,1); /* to store results */
call gagetval(value, id, 1); /* gets first value */
bestValue[1] = value;
do i = 2 to niter;
call garegen(id);
call gagetval(value, id, 1);
bestValue[i] = value;
end;
/* print solution history */
print (t(1:niter))[l = "iteration"] bestValue;
/* print final solution */
call gagetmem(bestMember, value, id, 1);
print "best member " bestMember [f = 3.0 l = ""],,
"final best value " value [l = ""];
call gaend(id);
For this test case, there is no call to GASETSEL. Therefore IML will use default selection parameters: an elite value of 1 and a conventional tournament of size 2. Also, since there is no GASETCRO or GASETMUT call, IML will use default genetic operators: the order operator for crossover and the invert operator for mutation, and a default mutation probability of 0.05. The output results are
iteration BESTVALUE
1 18
2 18
3 16
4 14
5 14
6 14
7 12
8 12
9 12
10 12
11 12
12 12
13 12
14 12
15 12
16 12
17 12
18 12
19 10
20 10
best member 10 1 2 3 4 5 6 7 8 9
final best value 10
The optimal value was reached after 19 iterations. Because the elite value was 1, the best solution was retained and passed on to each successive generation, and therefore never lost. Note that out of 3,628,800 possible solutions (representing 362,800 unique paths), the GA found the optimum after only 1,900 function evaluations, without using any problem-specific information to assist the optimization. You could also do some experimentation, and specify different genetic operators with a GASETCRO and GASETMUT call, and different selection parameters with a GASETSEL call:
/* alternate problem setup */
id = gasetup(3, /* 3 -> integer sequence encoding */
10, /* number of locations */
1234 /* initial seed */
);
/* set objective function */
call gasetobj(id,
2, /* 2 -> Traveling Salesman Problem */
coeffs /* cost coefficient matrix */
);
call gasetcro(id,
1.0, /* crossover probabilty 1 */
5 /* 5 -> pmatch operator */
);
call gasetmut(id,
0.05, /* mutation probability */
3 /* 3 -> swap operator */
);
call gasetsel(id,
3, /* set elite to 3 */
1, /* dual tournament */
0.95 /* best-player-wins probability 0.95 */
);
/* initialization phase */
call gainit(id,
100 /* initial population size */
);
/* execute regeneration loop */
niter = 15; /* number of iterations */
bestValue = j(niter,1); /* to store results */
call gagetval(value, id, 1); /* gets first value */
bestValue[1] = value;
do i = 2 to niter;
call garegen(id);
call gagetval(value, id, 1);
bestValue[i] = value;
end;
/* print solution history */
print (t(1:niter))[l = "iteration"] bestValue;
/* print final solution */
call gagetmem(bestMember, value, id, 1);
print "best member " bestMember [f = 3.0 l = ""],,
"final best value " value [l = ""];
call gaend(id);
The output of this test case is
iteration BESTVALUE
1 24
2 18
3 18
4 16
5 16
6 14
7 14
8 14
9 14
10 12
11 12
12 12
13 10
14 10
15 10
best member 3 4 5 6 7 8 9 10 1 2
final best value 10
Note that convergence was faster than for the previous case, reaching an optimum after 13 iterations. This illustrates that the convergence of a GA may be very sensitive to the choice of genetic operators and selection parameters, and for practical problems some experimental fine-tuning of optimization parameters may be required to obtain acceptable convergence.