Language Reference
CALL RZLIND (lindep, rup, bup, r <, sing> <, b> );
The RZLIND subroutine computes rank-deficient linear least squares solutions, complete orthogonal factorizations, and Moore-Penrose inverses.
The RZLIND subroutine returns the following values:
- lindep
-
is a scalar that contains the number of linear dependencies that are recognized in
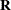 (number of zeroed rows in
(number of zeroed rows in rup[n,n]). - rup
-
is the updated
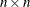 upper triangular matrix
upper triangular matrix 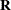 that contains zero rows corresponding to zero recognized diagonal elements in the original
that contains zero rows corresponding to zero recognized diagonal elements in the original 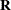 .
.
- bup
-
is the
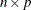 matrix
matrix 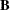 of right-hand sides that is updated simultaneously with
of right-hand sides that is updated simultaneously with 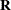 . If b is not specified, bup is not accessible.
. If b is not specified, bup is not accessible.
The input arguments to the RZLIND subroutine are as follows:
- r
-
specifies the
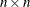 upper triangular matrix
upper triangular matrix 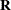 . Only the upper triangle of r is used; the lower triangle can contain any information.
. Only the upper triangle of r is used; the lower triangle can contain any information.
- sing
-
is an optional scalar that specifies a relative singularity criterion for the diagonal elements of
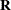 . The diagonal element
. The diagonal element 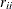 is considered zero if
is considered zero if 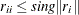 , where
, where 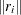 is the Euclidean norm of column
is the Euclidean norm of column  of
of 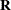 . If the value provided for sing is not positive, the default value sing
. If the value provided for sing is not positive, the default value sing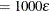 is used, where
is used, where  is the relative machine precision.
is the relative machine precision.
- b
-
specifies the optional
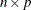 matrix
matrix 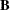 of right-hand sides that have to be updated or downdated simultaneously with
of right-hand sides that have to be updated or downdated simultaneously with 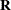 .
.
The singularity test used in the RZLIND subroutine is a relative test that uses the Euclidean norms of the columns ![]() of
of ![]() . The diagonal element
. The diagonal element ![]() is considered as nearly zero (and the ith row is zeroed out) if the following test is true:
is considered as nearly zero (and the ith row is zeroed out) if the following test is true:
Providing an argument sing![]() is the same as omitting the argument sing in the RZLIND call. In this case, the default is sing
is the same as omitting the argument sing in the RZLIND call. In this case, the default is sing![]() , where
, where ![]() is the relative machine precision. If
is the relative machine precision. If ![]() is computed by the QR decomposition
is computed by the QR decomposition ![]() , then the Euclidean norm of column i of
, then the Euclidean norm of column i of ![]() is the same (except for rounding errors) as the Euclidean norm of column i of
is the same (except for rounding errors) as the Euclidean norm of column i of ![]() .
.
Consider the following application of the RZLIND subroutine. Assume that you want to compute the upper triangular Cholesky
factor ![]() of the
of the ![]() positive semidefinite matrix
positive semidefinite matrix ![]() ,
,
The Cholesky factor ![]() of a positive definite matrix
of a positive definite matrix ![]() is unique (with the exception of the sign of its rows). However, the Cholesky factor of a positive semidefinite (singular)
matrix
is unique (with the exception of the sign of its rows). However, the Cholesky factor of a positive semidefinite (singular)
matrix ![]() can have many different forms.
can have many different forms.
In the following example, ![]() is a
is a ![]() matrix with linearly dependent columns
matrix with linearly dependent columns ![]() and
and ![]() with
with ![]() ,
, ![]() , and
, and ![]() .
.
proc iml;
a = {1 1 0 0 1 0 0,
1 1 0 0 1 0 0,
1 1 0 0 0 1 0,
1 1 0 0 0 0 1,
1 0 1 0 1 0 0,
1 0 1 0 0 1 0,
1 0 1 0 0 1 0,
1 0 1 0 0 0 1,
1 0 0 1 1 0 0,
1 0 0 1 0 1 0,
1 0 0 1 0 0 1,
1 0 0 1 0 0 1};
a = a || uniform(j(nrow(a),1,1));
aa = a` * a;
m = nrow(a); n = ncol(a);
Applying the ROOT function
to the coefficient matrix ![]() of the normal equations generates an upper triangular matrix
of the normal equations generates an upper triangular matrix ![]() in which linearly dependent rows are zeroed out. The following statements verify that
in which linearly dependent rows are zeroed out. The following statements verify that ![]() :
:
r1 = root(aa); ss1 = ssq(aa - r1` * r1); print ss1 r1[format=best6.];
Applying the QR subroutine with column pivoting on the original matrix ![]() yields a different result, but you can also verify
yields a different result, but you can also verify ![]() after pivoting the rows and columns of
after pivoting the rows and columns of ![]() :
:
ord = j(n,1,0); call qr(q,r2,pivqr,lindqr,a,ord); ss2 = ssq(aa[pivqr,pivqr] - r2` * r2); print ss2 r2[format=best6.];
Figure 24.336: A QR Decomposition
| ss2 | r2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 3.067E-29 | -3.464 | -1.155 | -1.155 | -1.155 | -1.155 | -1.801 | -1.155 | -1.155 |
| 0 | -1.633 | 0.2041 | -0.408 | 0.8165 | -0.029 | 0.8165 | 0.2041 | |
| 0 | 0 | 1.6202 | -0.772 | 0.3086 | -0.379 | -0.309 | -0.849 | |
| 0 | 0 | 0 | -1.38 | -0.173 | 0.4128 | 0.1725 | 1.3801 | |
| 0 | 0 | 0 | 0 | -1.369 | -0.194 | 1.3693 | 18E-17 | |
| 0 | 0 | 0 | 0 | 0 | -0.961 | -5E-17 | 52E-18 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Using the RUPDT subroutine
for stepwise updating of ![]() by the m rows of
by the m rows of ![]() results in an upper triangular matrix
results in an upper triangular matrix ![]() with
with ![]() nearly zero diagonal elements. However, other elements in rows with nearly zero diagonal elements can have significant values.
The following statements verify that
nearly zero diagonal elements. However, other elements in rows with nearly zero diagonal elements can have significant values.
The following statements verify that ![]() :
:
r3 = shape(0,n,n); call rupdt(rup,bup,sup,r3,a); r3 = rup; ss3 = ssq(aa - r3` * r3); print ss3 r3[format=best6.];
Figure 24.337: An Updated Matrix
| ss3 | r3 | |||||||
|---|---|---|---|---|---|---|---|---|
| 4.4E-29 | 3.4641 | 1.1547 | 1.1547 | 1.1547 | 1.1547 | 1.1547 | 1.1547 | 1.8012 |
| 0 | -1.633 | 0.8165 | 0.8165 | -0.408 | 0.2041 | 0.2041 | 0.1626 | |
| 0 | 0 | -1.414 | 1.4142 | -6E-17 | -0.354 | 0.3536 | -0.532 | |
| 0 | 0 | 0 | 5E-16 | 0.3739 | 0.3484 | -0.722 | 0.0906 | |
| 0 | 0 | 0 | 0 | -1.536 | 0.8984 | 0.6379 | -0.052 | |
| 0 | 0 | 0 | 0 | 0 | 1.2536 | -1.254 | -0.246 | |
| 0 | 0 | 0 | 0 | 0 | 0 | -4E-16 | -0.168 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9316 | |
The result ![]() of the RUPDT subroutine
can be transformed into the result
of the RUPDT subroutine
can be transformed into the result ![]() of the ROOT function
by left applications of Givens rotations to zero out the remaining significant elements of rows with small diagonal elements. Applying the RZLIND subroutine to the upper triangular result
of the ROOT function
by left applications of Givens rotations to zero out the remaining significant elements of rows with small diagonal elements. Applying the RZLIND subroutine to the upper triangular result ![]() of the RUPDT subroutine
generates a Cholesky factor
of the RUPDT subroutine
generates a Cholesky factor ![]() with rows of zeros that correspond to diagonal elements that are small. This gives the same result as the ROOT function
(except for the sign of rows) if its singularity criterion recognizes the same linear dependencies.
with rows of zeros that correspond to diagonal elements that are small. This gives the same result as the ROOT function
(except for the sign of rows) if its singularity criterion recognizes the same linear dependencies.
call rzlind(lind,r4,bup,r3); ss4 = ssq(aa - r4` * r4); print ss4 r4[format=best6.];
Consider the rank-deficient linear least squares problem:
For ![]() , the optimal solution,
, the optimal solution, ![]() , is unique; however, for
, is unique; however, for ![]() , the rank-deficient linear least squares problem has many optimal solutions, each of which has the same least squares residual
sum of squares:
, the rank-deficient linear least squares problem has many optimal solutions, each of which has the same least squares residual
sum of squares:
The solution of the full-rank problem, ![]() , is illustrated in the section The Full-Rank Linear Least Squares Problem. The following example demonstrates how to compute several solutions to the singular problem. The example uses the
, is illustrated in the section The Full-Rank Linear Least Squares Problem. The following example demonstrates how to compute several solutions to the singular problem. The example uses the ![]() matrix from the preceding section and generates a new column vector b. The vector b and the matrix
matrix from the preceding section and generates a new column vector b. The vector b and the matrix ![]() are shown in the output.
are shown in the output.
b = uniform(j(12,1,1)); ab = a` * b; print b a[format=best6.];
Figure 24.339: Singular Data
| b | a | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.8533943 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0.185 |
| 0.0671846 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0.9701 |
| 0.9570239 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0.3998 |
| 0.297194 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0.2594 |
| 0.2726118 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0.9216 |
| 0.6899296 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.9693 |
| 0.9767649 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.543 |
| 0.2265075 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0.5317 |
| 0.6882366 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0.0498 |
| 0.4127639 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0.0666 |
| 0.5585541 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0.8193 |
| 0.2872256 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0.5239 |
The rank-deficient linear least squares problem can be solved in the following ways. Although each method minimizes the residual sum of squares, not all of the given solutions are of minimum Euclidean length.
You can solve the rank-deficient least squares problem by using the singular value decomposition of ![]() , given by
, given by ![]() . Take the reciprocals of significant singular values and set the small values of
. Take the reciprocals of significant singular values and set the small values of ![]() to zero.
to zero.
call svd(u,d,v,a); t = 1e-12 * d[1]; do i=1 to n; if d[i] < t then d[i] = 0.; else d[i] = 1. / d[i]; end; x1 = v * diag(d) * u` * b; len1 = x1` * x1; ss1 = ssq(a * x1 - b); x1 = x1`; print ss1 len1, x1[format=best6.];
The solution ![]() obtained by singular value decomposition,
obtained by singular value decomposition, ![]() , is of minimum Euclidean length.
, is of minimum Euclidean length.
You can solve the rank-deficient least squares problem by using the QR decomposition with column pivoting:
Set the right part ![]() to zero and invert the upper triangular matrix
to zero and invert the upper triangular matrix ![]() to obtain a generalized inverse
to obtain a generalized inverse ![]() and an optimal solution
and an optimal solution ![]() :
:
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,1:nr]; x2 = shape(0,n,1); x2[pivqr] = trisolv(1,r,qtb[1:nr]) // j(lindqr,1,0.); len2 = x2` * x2; ss2 = ssq(a * x2 - b); x2 = x2`; print ss2 len2, x2 [format=best6.];
Notice that the residual sum of squares is minimal, but the solution ![]() is not of minimum Euclidean length.
is not of minimum Euclidean length.
You can solve the rank-deficient least squares problem by using the result ![]() of the ROOT function
to obtain the vector piv which indicates the zero rows in the upper triangular matrix
of the ROOT function
to obtain the vector piv which indicates the zero rows in the upper triangular matrix ![]() :
:
r1 = root(aa);
nr = n - lind;
piv = shape(0,n,1);
j1 = 1; j2 = nr + 1;
do i=1 to n;
if r1[i,i] ^= 0 then do;
piv[j1] = i; j1 = j1 + 1;
end;
else do;
piv[j2] = i; j2 = j2 + 1;
end;
end;
Now compute ![]() by solving the equation
by solving the equation ![]() .
.
r = r1[piv[1:nr],piv[1:nr]]; x = trisolv(2,r,ab[piv[1:nr]]); x = trisolv(1,r,x); x3 = shape(0,n,1); x3[piv] = x // j(lind,1,0.); len3 = x3` * x3; ss3 = ssq(a * x3 - b); x3 = x3`; print ss3 len3, x3[format=best6.];
Note that the residual sum of squares is minimal, but the solution ![]() is not of minimum Euclidean length.
is not of minimum Euclidean length.
You can solve the rank-deficient least squares problem by using the result ![]() of the RUPDT call
on and the vector piv (obtained in the previous solution), which indicates the zero rows of upper triangular matrices
of the RUPDT call
on and the vector piv (obtained in the previous solution), which indicates the zero rows of upper triangular matrices ![]() and
and ![]() . After zeroing out the rows of
. After zeroing out the rows of ![]() belonging to small diagonal pivots, solve the system
belonging to small diagonal pivots, solve the system ![]() .
.
r3 = shape(0,n,n); qtb = shape(0,n,1); call rupdt(rup,bup,sup,r3,a,qtb,b); r3 = rup; qtb = bup; call rzlind(lind,r4,bup,r3,,qtb); qtb = bup[piv[1:nr]]; x = trisolv(1,r4[piv[1:nr],piv[1:nr]],qtb); x4 = shape(0,n,1); x4[piv] = x // j(lind,1,0.); len4 = x4` * x4; ss4 = ssq(a * x4 - b); x4 = x4`; print ss4 len4, x4[format=best6.];
Because the matrices ![]() and
and ![]() are the same (except for the signs of rows), the solution
are the same (except for the signs of rows), the solution ![]() is the same as
is the same as ![]() .
.
You can solve the rank-deficient least squares problem by using the result ![]() of the RZLIND subroutine in the previous solution, which is the result of the first step of complete QR decomposition, and perform the second step of complete QR decomposition. The rows of matrix
of the RZLIND subroutine in the previous solution, which is the result of the first step of complete QR decomposition, and perform the second step of complete QR decomposition. The rows of matrix ![]() can be permuted to the upper trapezoidal form
can be permuted to the upper trapezoidal form
where ![]() is nonsingular and upper triangular and
is nonsingular and upper triangular and ![]() is rectangular. Next, perform the second step of complete QR decomposition with the lower triangular matrix
is rectangular. Next, perform the second step of complete QR decomposition with the lower triangular matrix
which leads to the upper triangular matrix ![]() .
.
r = r4[piv[1:nr],]`; call qr(q,r5,piv2,lin2,r); y = trisolv(2,r5,qtb); x5 = q * (y // j(lind,1,0.)); len5 = x5` * x5; ss5 = ssq(a * x5 - b); x5 = x5`; print ss5 len5, x5[format=best6.];
The solution ![]() obtained by complete QR decomposition has minimum Euclidean length.
obtained by complete QR decomposition has minimum Euclidean length.
You can solve the rank-deficient least squares problem by performing both steps of complete QR decomposition. The first step
performs the pivoted QR decomposition of ![]() ,
,
where ![]() is nonsingular and upper triangular and
is nonsingular and upper triangular and ![]() is rectangular. The second step performs a QR decomposition as described in the previous method. This results in
is rectangular. The second step performs a QR decomposition as described in the previous method. This results in
where ![]() is lower triangular.
is lower triangular.
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,]`; call qr(q,r5,piv2,lin2,r); y = trisolv(2,r5,qtb[1:nr]); x6 = shape(0,n,1); x6[pivqr] = q * (y // j(lindqr,1,0.)); len6 = x6` * x6; ss6 = ssq(a * x6 - b); x6 = x6`; print ss6 len6, x6[format=best6.];
The solution ![]() obtained by complete QR decomposition has minimum Euclidean length.
obtained by complete QR decomposition has minimum Euclidean length.
You can solve the rank-deficient least squares problem by performing a complete QR decomposition with the QR and LUPDT calls :
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`; call lupdt(lup,bup,sup,r,z); rd = trisolv(3,lup,r2[1:nr,]); rd = trisolv(4,lup,rd); x7 = shape(0,n,1); x7[pivqr] = rd` * qtb[1:nr,]; len7 = x7` * x7; ss7 = ssq(a * x7 - b); x7 = x7`; print ss7 len7, x7[format=best6.];
The solution ![]() obtained by complete QR decomposition has minimum Euclidean length.
obtained by complete QR decomposition has minimum Euclidean length.
You can solve the rank-deficient least squares problem by performing a complete QR decomposition with the RUPDT , RZLIND, and LUPDT calls :
r3 = shape(0,n,n); qtb = shape(0,n,1); call rupdt(rup,bup,sup,r3,a,qtb,b); r3 = rup; qtb = bup; call rzlind(lind,r4,bup,r3,,qtb); nr = n - lind; qtb = bup; r = r4[piv[1:nr],piv[1:nr]]`; z = r4[piv[1:nr],piv[nr+1:n]]`; call lupdt(lup,bup,sup,r,z); rd = trisolv(3,lup,r4[piv[1:nr],]); rd = trisolv(4,lup,rd); x8 = shape(0,n,1); x8 = rd` * qtb[piv[1:nr],]; len8 = x8` * x8; ss8 = ssq(a * x8 - b); x8 = x8`; print ss8 len8, x8[format=best6.];
The solution ![]() obtained by complete QR decomposition has minimum Euclidean length. The same result can be obtained with the APPCORT call
or the COMPORT call
.
obtained by complete QR decomposition has minimum Euclidean length. The same result can be obtained with the APPCORT call
or the COMPORT call
.
You can use various orthogonal methods to compute the Moore-Penrose inverse ![]() of a rectangular matrix
of a rectangular matrix ![]() . The following examples find the Moore-Penrose inverse of the matrix
. The following examples find the Moore-Penrose inverse of the matrix ![]() shown in section A Cholesky Root.
shown in section A Cholesky Root.
You can find the Moore-Penrose inverse by using the GINV function
. The GINV function uses the singular decomposition ![]() . The result
. The result ![]() should be identical to the result given by the next solution.
should be identical to the result given by the next solution.
ga = ginv(a);
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss1 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss1, ga[format=best6.];
Figure 24.348: Moore-Penrose Inverse
| ga | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| COL1 | COL2 | COL3 | COL4 | COL5 | COL6 | COL7 | COL8 | COL9 | COL10 | COL11 | COL12 | |
| ROW1 | 0.1483 | -0.117 | 0.0366 | 0.1318 | 0.0066 | -0.049 | 0.0952 | 0.1469 | 0.1618 | 0.1169 | -0.089 | 0.0105 |
| ROW2 | 0.1595 | 0.1339 | 0.2154 | 0.2246 | -0.121 | -0.06 | -0.046 | -0.041 | -0.106 | -0.044 | -0.063 | -0.054 |
| ROW3 | 0.0593 | -0.235 | -0.132 | 0.041 | 0.1684 | 0.0403 | 0.2002 | 0.3244 | 0.0743 | -0.042 | -0.205 | -0.094 |
| ROW4 | -0.07 | -0.015 | -0.047 | -0.134 | -0.041 | -0.029 | -0.059 | -0.137 | 0.1934 | 0.2027 | 0.179 | 0.1582 |
| ROW5 | 0.1923 | 0.0783 | -0.122 | -0.081 | 0.198 | -0.092 | -0.031 | -0.008 | 0.2647 | -0.021 | -0.11 | -0.067 |
| ROW6 | -0.044 | -0.06 | 0.2159 | -0.045 | -0.119 | 0.1443 | 0.1526 | -0.111 | -0.044 | 0.2205 | -0.058 | -0.052 |
| ROW7 | 0.0004 | -0.135 | -0.057 | 0.2586 | -0.072 | -0.101 | -0.027 | 0.2663 | -0.059 | -0.082 | 0.0787 | 0.1298 |
| ROW8 | -0.315 | 0.5343 | 0.0431 | -0.262 | 0.1391 | 0.3163 | -0.145 | -0.311 | -0.358 | -0.215 | 0.4462 | 0.1266 |
You can find the Moore-Penrose inverse by using the singular value decomposition. The singular decomposition ![]() with
with ![]() ,
, ![]() , and
, and ![]() , can be used to compute
, can be used to compute ![]() , with
, with ![]() and
and
The result ![]() should be the same as that given by the GINV function
if the singularity criterion
should be the same as that given by the GINV function
if the singularity criterion ![]() is selected correspondingly. Since you cannot specify the criterion
is selected correspondingly. Since you cannot specify the criterion ![]() for the GINV function, the singular value decomposition approach can be important for applications where the GINV function
uses an unsuitable
for the GINV function, the singular value decomposition approach can be important for applications where the GINV function
uses an unsuitable ![]() criterion. The slight discrepancy between the values of SS1 and SS2 is due to rounding that occurs in the statement that
computes the matrix GA.
criterion. The slight discrepancy between the values of SS1 and SS2 is due to rounding that occurs in the statement that
computes the matrix GA.
call svd(u,d,v,a);
do i=1 to n;
if d[i] <= 1e-10 * d[1] then d[i] = 0.;
else d[i] = 1. / d[i];
end;
ga = v * diag(d) * u`;
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss2 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss2;
You can find the Moore-Penrose inverse by using the complete QR decomposition. The complete QR decomposition
where ![]() is lower triangular, yields the Moore-Penrose inverse
is lower triangular, yields the Moore-Penrose inverse
ord = j(n,1,0);
call qr(q1,r2,pivqr,lindqr,a,ord);
nr = n - lindqr;
q1 = q1[,1:nr]; r = r2[1:nr,]`;
call qr(q2,r5,piv2,lin2,r);
tt = trisolv(4,r5`,q1`);
ga = shape(0,n,m);
ga[pivqr,] = q2 * (tt // shape(0,n-nr,m));
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss3 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss3;
You can find the Moore-Penrose inverse by using the complete QR decomposition with QR and LUPDT :
ord = j(n,1,0);
call qr(q,r2,pivqr,lindqr,a,ord);
nr = n - lindqr;
r = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r2[1:nr,]);
rd = trisolv(4,lup,rd);
ga = shape(0,n,m);
ga[pivqr,] = rd` * q[,1:nr]`;
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss4 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss4;
You can find the Moore-Penrose inverse by using the complete QR decomposition with the RUPDT call and the LUPDT call :
r3 = shape(0,n,n);
y = i(m); qtb = shape(0,n,m);
call rupdt(rup,bup,sup,r3,a,qtb,y);
r3 = rup; qtb = bup;
call rzlind(lind,r4,bup,r3,,qtb);
nr = n - lind; qtb = bup;
r = r4[piv[1:nr],piv[1:nr]]`;
z = r4[piv[1:nr],piv[nr+1:n]]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r4[piv[1:nr],]);
rd = trisolv(4,lup,rd);
ga = shape(0,n,m);
ga = rd` * qtb[piv[1:nr],];
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss5 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss5;