Language Reference
CALL NLPDD (rc, xr, "fun", x0 <*>, opt <*>, blc <*>, tc <*>, par <*>, "ptit" <*>, "grd" );
The NLPDD subroutine uses the double-dogleg method to solve a nonlinear optimization problem.
See the section Nonlinear Optimization and Related Subroutines for a listing of all NLP subroutines. See Chapter 14 for a description of the arguments of NLP subroutines.
The double-dogleg optimization method combines the ideas of the quasi-Newton and trust-region methods. In each iteration,
the algorithm computes the step, ![]() , as a linear combination of the steepest descent or ascent search direction,
, as a linear combination of the steepest descent or ascent search direction, ![]() , and a quasi-Newton search direction,
, and a quasi-Newton search direction, ![]() , as follows:
, as follows:
The step ![]() must remain within a specified trust-region radius (Fletcher, 1987). Hence, the NLPDD subroutine uses the dual quasi-Newton update but does not perform a line search. You can specify one of
two update formulas with the fourth element of the opt input argument.
must remain within a specified trust-region radius (Fletcher, 1987). Hence, the NLPDD subroutine uses the dual quasi-Newton update but does not perform a line search. You can specify one of
two update formulas with the fourth element of the opt input argument.
|
Value of opt[4] |
Update Method |
|---|---|
|
1 |
Dual BFGS update of the Cholesky factor of the Hessian matrix. |
|
This is the default. |
|
|
2 |
Dual DFP update of the Cholesky factor of the Hessian matrix. |
The double-dogleg optimization technique works well for medium to moderately large optimization problems, in which the objective function and the gradient are much faster to compute than the Hessian. The implementation is based on Dennis and Mei (1979) and Gay (1983), but it is extended for boundary and linear constraints. The NLPDD subroutine generally needs more iterations than the techniques that require second-order derivatives (NLPTR , NLPNRA , and NLPNRR ), but each of the NLPDD iterations is computationally inexpensive. Furthermore, the NLPDD subroutine needs only gradient calls to update the Cholesky factor of an approximate Hessian.
In addition to the standard iteration history, the NLPDD routine prints the following information:
-
The heading lambda refers to the parameter
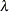 of the double-dogleg step. A value of 0 corresponds to the full (quasi-) Newton step.
of the double-dogleg step. A value of 0 corresponds to the full (quasi-) Newton step.
-
The heading slope refers to
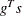 , the slope of the search direction at the current parameter iterate
, the slope of the search direction at the current parameter iterate 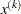 . For minimization, this value should be significantly smaller than zero.
. For minimization, this value should be significantly smaller than zero.
The following statements invoke the NLPDD subroutine to solve the constrained Betts optimization problem (see the section Constrained Betts Function):
start F_BETTS(x);
f = .01 * x[1] * x[1] + x[2] * x[2] - 100;
return(f);
finish F_BETTS;
con = { 2 -50 . .,
50 50 . .,
10 -1 1 10};
x = {-1 -1};
opt = {0 1};
call nlpdd(rc, xres, "F_BETTS", x, opt, con);
Figure 24.232 shows the iteration history. The optimization converged after six iterations.
Figure 24.232: Constrained Optimization
| Note: | Initial point was changed to be feasible for boundary and linear constraints. |
| Double Dogleg Optimization |
| Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS) |
| Without Parameter Scaling |
| Gradient Computed by Finite Differences |
| Parameter Estimates | 2 |
|---|---|
| Lower Bounds | 2 |
| Upper Bounds | 2 |
| Linear Constraints | 1 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Slope of Search Direction |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 0 | -99.54678 | 1.0092 | 0.1346 | 6.012 | -1.805 | ||
| 2 | 0 | 3 | 0 | -99.59120 | 0.0444 | 0.1279 | 0 | -0.0228 | ||
| 3 | 0 | 5 | 0 | -99.90252 | 0.3113 | 0.0624 | 0 | -0.209 | ||
| 4 | 0 | 6 | 1 | -99.96000 | 0.0575 | 0.00432 | 0 | -0.0975 | ||
| 5 | 0 | 7 | 1 | -99.96000 | 4.66E-6 | 0.000079 | 0 | -458E-8 | ||
| 6 | 0 | 8 | 1 | -99.96000 | 1.559E-9 | 0 | 0 | -16E-10 |
The optimal value for the function is returned in the xres vector, which is displayed in Figure 24.233.