Language Reference

MARG Call

CALL MARG (locmar, marginal, dim, table, config);

The MARG subroutine evaluates marginal totals in a multiway contingency table.

The input arguments to the MARG subroutine are as follows:

locmar: is a returned matrix that contains a vector of indices to each new set of marginal totals under the model specified by config. A marginal total is exhibited for each level of the specified marginal. These indices help locate particular totals.
marginal: is a return vector of marginal totals.
dim: is an input matrix. If the problem contains v variables, then dim is 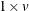$1 \times v$ row vector. The value dim[i] is the number of possible levels for variable i in a contingency table.
table: is an input matrix. The table argument specifies an array of the number of observations at each level of each variable. Variables are nested across columns and then across rows.
config: is an input matrix. The config argument specifies which marginal totals to evaluate. Each column of config specifies a distinct marginal in the model under consideration.

The matrix table must conform in size to the contingency table specified in dim. In particular, if table is $n \times m$ , the product of the entries in the dim vector must equal $nm$ . In addition, there must be some integer k such that the product of the first k entries in dim equals m. See the description of the IPF function for more information about specifying table.

For example, consider the three-dimensional table discussed in the IPF call , based on data that appear in Christensen (1997). The table presents data on a person’s self-esteem for people classified according to their religion and their father’s educational level.

		Father’s Educational Level
	Self-	Not HS	HS	Some	Coll	Post
Religion	Esteem	Grad	Grad	Coll	Grad	Coll
	High	575	388	100	77	51
Catholic
	Low	267	153	40	37	19
	High	117	102	67	87	62
Jewish
	Low	48	35	18	12	13
	High	359	233	109	197	90
Protestant
	Low	159	173	47	82	32

As explained in the IPF call documentation, the father’s education level is Variable 1, self-esteem is Variable 2, and religion is Variable 3.

The following program encodes this table, uses the MARG call to compute a two-way marginal table by summing over the third variable and a one-way marginal by summing over the first two variables.

dim={5 2 3};

table={
/* Father's Education:
           NotHSGrad HSGrad Col ColGrad PostCol
          Self-
   Relig  Esteem                           */
/* Cath-   Hi */ 575   388  100    77   51,
/* olic    Lo */ 267   153   40    37   19,

/* Jew-    Hi */ 117   102   67    87   62,
/*  ish    Lo */  48    35   18    12   13,

/* Prot-   Hi */ 359   233  109   197   90,
/* estant  Lo */ 159   173   47    82   32
        };

config = { 1 3,
           2 0 };
call marg(locmar, marginal, dim, table, config);
print locmar, marginal;

Figure 24.206: Marginal Totals in a Three-Way Table

locmar
1	11

marginal
	COL1	COL2	COL3	COL4	COL5	COL6	COL7	COL8	COL9	COL10	COL11	COL12	COL13
ROW1	1051	723	276	361	203	474	361	105	131	64	1707	561	1481

The first marginal total is contained in locations 1 through 10 of the marginal vector, which is shown in Figure 24.206. It represents the results of summing table over the religion variable. The first entry of marginal is the number of subjects with high self-esteem whose fathers did not graduate from high school ( $1051 = 575 + 117 + 359$ ). The second entry is the number of subjects with high self-esteem whose fathers were high school graduates ( $723 = 388 + 102 + 233$ ). The tenth entry is the number of subjects with low self-esteem whose fathers had some post-collegiate education ( $64 = 19 + 13 + 32$ ).

The second marginal is contained in locations 11 through 13 of the marginal vector. It represents the results of summing table over the education and self-esteem variables. The eleventh entry of the marginal vector is the number of Catholics in the study. The thirteenth entry is the number of Protestants.

You can also extract the marginal totals into separate vectors, as shown in the following statements:

/* Examine marginals: The name indicates the
   variable(s) that are NOT summed over.
   The locmar variable tells where to index
   into the marginal variable. */
Var12_Marg = marginal[1:(locmar[2]-1)];
Var12_Marg = shape(Var12_Marg, dim[2], dim[1]);
Var3_Marg  = marginal[locMar[2]:ncol(marginal)];
print Var12_Marg, Var3_Marg;

Figure 24.207: Marginal Totals

Var12_Marg
1051	723	276	361	203
474	361	105	131	64

Var3_Marg
1707
561
1481