RDODT and RUPDT Calls :: SAS/IML(R) 13.1 User's Guide

RDODT and RUPDT Calls

CALL RDODT (def, rup, bup, sup, r, z <*>, b <*>, y <*>, ssq ) ;

CALL RUPDT (rup, bup, sup, r, z <*>, b <*>, y <*>, ssq ) ;

If $\bA = \bQ \bR$ is the QR decomposition of the matrix $\bA$ , the RUPDT subroutine enables you to efficiently recompute the $\mb {R}$ matrix when a new row is added to $A$ . This is called an update. Similarly, the RDODT subroutine enables you to efficiently recompute the $\mb {R}$ matrix when an existing row is deleted from $A$ . This is called a downdate. You can also use the RDODT and RUPDT subroutines to downdate and update Cholesky decompositions.

The RDODT and RUPDT subroutines return the values:

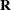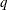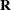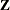def: is only used for downdating, and it specifies whether the downdating of matrix $\mathbf{R}$ by using the $q$ rows in argument z has been successful. The result def=2 means that the downdating of $\mathbf{R}$ by at least one row of $\mathbf{Z}$ leads to a singular matrix and cannot be completed successfully (since the result of downdating is not unique). In that case, the results rup, bup, and sup contain missing values only. The result def=1 means that the residual sum of squares, ssq, could not be downdated successfully and the result sup contains missing values only. 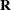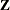The result def=0 means that the downdating of $\mathbf{R}$ by $\mathbf{Z}$ was completed successfully.
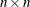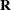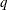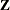rup: is the $n \times n$ upper triangular matrix $\mathbf{R}$ that has been updated or downdated by using the $q$ rows in $\mathbf{Z}$ .
bup: is the 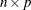$n \times p$ matrix 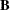$\mathbf{B}$ of right-hand sides that has been updated or downdated by using the 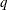$q$ rows in argument y. If the argument b is not specified, bup is not computed.
sup: is a 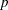$p$ vector of square roots of residual sum of squares that is updated or downdated by using the 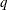$q$ rows of argument y. If ssq is not specified, sup is not computed.

The input arguments to the RDODT and RUPDT subroutines are as follows:

r: specifies an 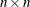$n \times n$ upper triangular matrix 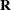$\mathbf{R}$ to be updated or downdated by the 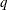$q$ rows in 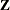$\mathbf{Z}$ . Only the upper triangle of 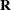$\mathbf{R}$ is used; the lower triangle can contain any information.
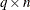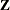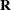z: specifies a $q \times n$ matrix $\mathbf{Z}$ used rowwise to update or downdate the matrix $\mathbf{R}$ .
b: specifies an optional 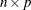$n \times p$ matrix 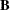$\mathbf{B}$ of right-hand sides that have to be updated or downdated simultaneously with 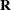$\mathbf{R}$ . If b is specified, the argument y must also be specified.
y: specifies an optional 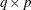$q \times p$ matrix 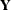$\mathbf{Y}$ used rowwise to update or downdate the right-hand side matrix 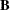$\mathbf{B}$ . If b is specified, the argument y must also be specified.
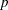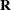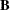ssq: is an optional $p$ vector that, if b is specified, specifies the square root of the error sum of squares that should be updated or downdated simultaneously with $\mathbf{R}$ and $\mathbf{B}$ .

The upper triangular matrix $\mathbf{R}$ of the QR decomposition of an $m \times n$ matrix $\mathbf{A}$ ,

$\bA = \bQ \bR , \mbox{ where } \bQ ^{\prime } \bQ = \bQ \bQ ^{\prime } = \bI _ m$

is recomputed efficiently in two cases:

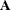update: An $n$ vector z is added to matrix $\mathbf{A}$ .
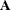downdate: An $n$ vector z is deleted from matrix $\mathbf{A}$ .

Computing the whole QR decomposition of matrix $\mathbf{A}$ by Householder transformations requires $4mn^2 - 4n^3/3$ floating-point operations, whereas updating or downdating the QR decomposition (by Givens rotations) of one row vector z requires only $2n^2$ floating-point operations.

If the QR decomposition is used to solve the full-rank linear least squares problem

$\min _{x} \| \mathbf{A} x - b \| ^2 = \mbox{ssq}$

by solving the nonsingular upper triangular system

$x = \mathbf{R}^{-1} \mathbf{Q}^{\prime } b$

then the RUPDT and RDODT subroutines can be used to update or downdate the $p$ -transformed right-hand sides $\mathbf{Q}^{\prime } \mathbf{B}$ and the residual sum-of-squares $p$ vector ssq provided that for each $n$ vector z added to or deleted from $\mathbf{A}$ there is also a $p$ vector y added to or deleted from the $m \times p$ right-hand-side matrix $\mathbf{B}$ .

If the arguments z and y of the subroutines RUPDT and RDODT contain $q > 1$ row vectors for which $\mathbf{R}$ (and $\mathbf{Q}^{\prime } \mathbf{B}$ , and eventually ssq) is to be updated or downdated, the process is performed stepwise by processing the rows z $_ k$ (and y $_ k$ ), $k = 1,\ldots ,q$ , in the order in which they are stored.

The QR decomposition of an $m \times n$ matrix $\mathbf{A}$ , $m \geq n$ , rank $(\mathbf{A}) = n$ ,

$\mathbf{A} = \mathbf{Q} \mathbf{R}, \mbox{ where } \mathbf{Q}^{\prime } \mathbf{Q} = \mathbf{Q} \mathbf{Q}^{\prime } = \mathbf{I}_ m$

corresponds to the Cholesky factorization

$\mathbf{C} = \mathbf{R}^{\prime } \mathbf{R}, \mbox{ where } \mathbf{C} = \mathbf{A}^{\prime } \mathbf{A}$

of the positive definite $n \times n$ crossproduct matrix $\mathbf{C} = \mathbf{A}^{\prime } \mathbf{A}$ . In the case where $m \geq n$ and rank $(\mathbf{A}) = n$ , the upper triangular matrix $\mathbf{R}$ computed by the QR decomposition (with positive diagonal elements) is the same as the one computed by Cholesky factorization except for numerical error,

$\mathbf{A}^{\prime } \mathbf{A} = (\mathbf{Q}\mathbf{R})^{\prime } (\mathbf{Q} \mathbf{R}) = \mathbf{R}^{\prime } \mathbf{R}$

Adding a row vector $z$ to matrix $\mathbf{A}$ corresponds to the rank-1 modification of the crossproduct matrix $\mathbf{C}$

$\mb {\widetilde{\mathbf{C}}} = \mathbf{C} + z^{\prime } z, \mbox{ where } \mb {\widetilde{\mathbf{C}}} = \mb {\widetilde{\mathbf{A}}^{\prime } \widetilde{\mathbf{A}}}$

and the $(m+1) \times n$ matrix $\mb {\widetilde{A}}$ contains all rows of $\mathbf{A}$ with the row z added.

Deleting a row vector z from matrix $\mathbf{A}$ corresponds to the rank-1 modification

$\mathbf{C}^* = \mathbf{C} - z^{\prime } z, \mbox{ where } \mathbf{C}^* = \mathbf{A}^{*\prime } \mathbf{A}^*$

and the $(m-1) \times n$ matrix $\mathbf{A}^*$ contains all rows of $\mathbf{A}$ with the row z deleted. Thus, you can also use the subroutines RUPDT and RDODT to update or downdate the Cholesky factor $\mathbf{R}$ of a positive definite crossproduct matrix $\mathbf{C}$ of $\mathbf{A}$ .

The process of downdating an upper triangular matrix $\mathbf{R}$ (and eventually a residual sum-of-squares vector ssq) is not always successful. First of all, the downdated matrix $\mathbf{R}$ could be rank-deficient. Even if the downdated matrix $\mathbf{R}$ is of full rank, the process of downdating can be ill-conditioned and does not work well if the downdated matrix is close (by rounding errors) to a rank-deficient one. In these cases, the downdated matrix $\mathbf{R}$ is not unique and cannot be computed by subroutine RDODT. If $\mathbf{R}$ cannot be computed, def returns 2, and the results rup, bup, and sup return missing values.

The downdating of the residual sum-of-squares vector ssq can be a problem, too. In practice, the downdate formula

$\mbox{\Argument{ssq}}_{\mbox{new}} = \sqrt {{\mbox{\Argument{ssq}}}_{\mbox{old}} - {\mbox{\Argument{ssq}}}_{\mbox{dod}}}$

cannot always be computed because, due to rounding errors, the radicand can be negative. In this case, the result vector sup returns missing values, and def returns 1.

You can use various methods to compute the $p$ columns $x_ k$ of the $n \times p$ matrix $\mathbf{X}$ that minimize the $p$ linear least squares problems with an $m \times n$ coefficient matrix $\mathbf{A}$ , $m\geq n$ , rank $(\mathbf{A})=n$ , and $p$ right-hand-side vectors b $_ k$ (stored columnwise in the $m \times p$ matrix $\mathbf{B}$ ).

The methods in this section use the following simple example:

 a = { 1 3 ,
       2 2 ,
       3 1 };
 b = { 1, 1, 1};
 m = nrow(a);
 n = ncol(a);
 p = ncol(b);

Cholesky decomposition of crossproduct matrix:

/* form and solve the normal equations */
aa = a` * a; ab = a` * b;
r  = root(aa);
x  = trisolv(2,r,ab);
x  = trisolv(1,r,x);
print x;

QR decomposition by Householder transformations:

call qr(qtb, r, piv, lindep, a, , b);
x = trisolv(1, r[,piv], qtb[1:n,]);

Stepwise update by Givens rotations:

r = j(n,n,0); qtb = j(n,p,0); ssq = j(1,p,0);
do i = 1 to m;
   z = a[i,];
   y = b[i,];
   call rupdt(rup,bup,sup,r,z,qtb,y,ssq);
   r   = rup;
   qtb = bup;
   ssq = sup;
end;
x = trisolv(1,r,qtb);

Or, equivalently:

r   = j(n,n,0); qtb = j(n,p,0); ssq = j(1,p,0);
call rupdt(rup,bup,sup,r,a,qtb,b,ssq);
x   = trisolv(1,rup,bup);

Singular value decomposition:

call svd(u, d, v, a);
d = diag(1 / d);
x = v * d * u` * b;

For the preceding $3 \times 2$ example matrix a, each method obtains the unique LS estimator:

ss = ssq(a * x - b);
print ss x;

Figure 24.318: Least Squares Solution and Sum of Squared Residuals

ss	x
2.465E-31	0.25
	0.25

To compute the (transposed) matrix $\mathbf{Q}$ , you can use the following technique:

r = repeat(0,n,n);
y = i(m);
qt = repeat(0,n,m);
call rupdt(rup, qtup, sup, r, a, qt, y);
print qtup;

Figure 24.319: Transposed Matrix

qtup
0.2672612	0.5345225	0.8017837
-0.872872	-0.218218	0.4364358