FARMAFIT Call :: SAS/IML(R) 13.1 User's Guide

Previous Page|Next Page

FARMAFIT Call

CALL FARMAFIT (d, phi, theta, sigma, series <*>, p <*>, q <*>, opt ) ;

The FARMAFIT subroutine estimates the parameters of an ARFIMA( $p,d,q$ ) model.

The input arguments to the FARMAFIT subroutine are as follows:

series

specifies a time series (assuming mean zero).

p

specifies the set or subset of the AR order. If you do not specify p, the default is p $=0$ .

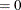If you specify p=3, the FARMAFIT subroutine estimates the coefficient of the lagged variable $y_{t-3}$ .

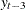If you specify p= 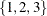$\{ 1,2,3\}$ , the FARMAFIT subroutine estimates the coefficients of lagged variables 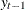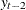$y_{t-1}$ , $y_{t-2}$ , and $y_{t-3}$ .

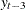q

specifies the subset of the MA order. If you do not specify q, the default value is 0.

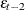If you specify q=2, the FARMAFIT subroutine estimates the coefficient of the lagged variable ${\epsilon }_{t-2}$ .

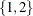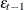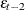If you specify q= $\{ 1,2\}$ , the FARMAFIT subroutine estimates the coefficients of lagged variables ${\epsilon }_{t-1}$ and ${\epsilon }_{t-2}$ .

opt

specifies the method of computing the log-likelihood function.

0: requests the conditional sum of squares function. This is the default.
1: requests the exact log-likelihood function. This option requires that the time series be stationary and invertible.

The FARMAFIT subroutine returns the following values:

d: is a scalar that contains a fractional differencing order.
phi: is a vector that contains the autoregressive coefficients.
theta: is a vector that contains the moving average coefficients.
sigma: is a scalar that contains a variance of the innovation series.

As an example, consider the following ARFIMA( $1,0.3,1$ ) model:

$(1-0.5B)(1-B)^{0.3}y_ t = (1+0.1B){\epsilon }_ t$

In this model, ${\epsilon }_ t \sim NID(0,1)$ . The following statements estimate the parameters of this model:

d = 0.3;
phi = 0.5;
theta = -0.1;
call farmasim(yt, d, phi, theta) seed=1234;
call farmafit(d, ar, ma, sigma, yt) p=1 q=1;
print d ar ma sigma;

Figure 24.129: Parameter Estimates for a ARFIMA Model

d	ar	ma	sigma
0.3950157	0.5676217	-0.012339	1.2992989

The FARMAFIT subroutine estimates the parameters $d$ , $\phi (B)$ , $\theta (B)$ , and $\sigma _{\epsilon }^2$ of an ARFIMA( $p,d,q$ ) model. The log-likelihood function is solved by iterative numerical procedures such as the quasi-Newton optimization. The starting value $d$ is obtained by the approach of Geweke and Porter-Hudak (1983); the starting values of the AR and MA parameters are obtained from the least squares estimates.