The COMPORT subroutine provides the complete orthogonal decomposition by Householder transformations of a matrix ![]() .
.
The subroutine returns the following values:
- q
-
is a matrix. If
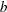 is not specified,
is not specified, 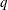 is the
is the  orthogonal matrix
orthogonal matrix 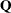 that is the product of the
that is the product of the 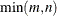 separate Householder transformations. If
separate Householder transformations. If 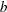 is specified,
is specified, 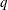 is the
is the 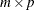 matrix
matrix 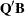 that has the transposed Householder transformations
that has the transposed Householder transformations 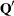 applied to the
applied to the 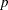 columns of the argument matrix
columns of the argument matrix 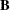 .
.
- r
-
is the
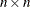 upper triangular matrix
upper triangular matrix 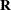 that contains the
that contains the  nonsingular upper triangular matrix
nonsingular upper triangular matrix 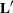 of the complete orthogonal decomposition, where
of the complete orthogonal decomposition, where 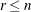 is the rank of
is the rank of 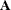 . The full
. The full  upper triangular matrix
upper triangular matrix 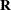 of the orthogonal decomposition of matrix
of the orthogonal decomposition of matrix 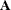 can be obtained by vertical concatenation of the
can be obtained by vertical concatenation of the 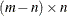 zero matrix to the result r.
zero matrix to the result r.
- p
-
is an
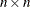 matrix that is the product
matrix that is the product 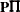 of a permutation matrix
of a permutation matrix 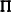 with an orthogonal matrix
with an orthogonal matrix 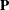 . The permutation matrix is determined by the vector piv.
. The permutation matrix is determined by the vector piv.
- piv
-
is an
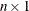 vector of permutations of the columns of
vector of permutations of the columns of 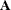 . That is, the QR decomposition is computed, not of
. That is, the QR decomposition is computed, not of 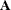 , but of the matrix with columns
, but of the matrix with columns ![$[\bA _{piv[1]}\ldots \bA _{piv[n]}]$](images/imlug_langref0184.png) . The vector piv corresponds to an
. The vector piv corresponds to an 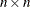 permutation matrix,
permutation matrix, 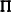 , of the pivoted QR decomposition in the first step of orthogonal decomposition.
, of the pivoted QR decomposition in the first step of orthogonal decomposition.
- lindep
-
specifies the number of linearly dependent columns in the matrix
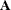 detected by applying the
detected by applying the  Householder transformation in the order specified by the argument piv. That is, lindep is
Householder transformation in the order specified by the argument piv. That is, lindep is  .
.
The input arguments to the COMPORT subroutine are as follows:
- a
-
specifies the
 matrix
matrix 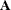 , with
, with 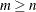 , which is to be decomposed into the product of the
, which is to be decomposed into the product of the  orthogonal matrix
orthogonal matrix 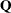 , the
, the 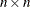 upper triangular matrix
upper triangular matrix 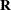 , and the
, and the 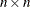 orthogonal matrix
orthogonal matrix 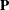 ,
,
![\[ \bA = \bQ \left[ \begin{array}{c} \bR \\ \mb {0} \end{array} \right] \bPi ^{\prime } \bP ^{\prime } \bPi \]](images/imlug_langref0060.png)
- b
-
specifies an optional
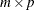 matrix
matrix 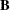 that is to be left-multiplied by the transposed
that is to be left-multiplied by the transposed  matrix
matrix 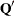 .
.
- sing
-
is an optional scalar that specifies a singularity criterion.
The complete orthogonal decomposition of the singular matrix ![]() can be used to compute the Moore-Penrose inverse
can be used to compute the Moore-Penrose inverse ![]() ,
, ![]() , or to compute the minimum Euclidean-norm solution of the rank-deficient least squares problem
, or to compute the minimum Euclidean-norm solution of the rank-deficient least squares problem ![]() .
.
-
Use the QR decomposition of
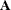 with column pivoting,
with column pivoting,
![\[ \bA = \bQ \left[ \begin{array}{c} \bR \\ \mb {0} \end{array} \right] \bPi ^{\prime } = \left[ \begin{array}{cc} \bY & \bZ \end{array} \right] \left[ \begin{array}{cc} \bR _1 & \bR _2 \\ \mb {0} & \mb {0} \end{array} \right] \bPi ^{\prime } \]](images/imlug_langref0191.png)
where
![$\bR = [ \begin{array}{cc} {\bR }_1 & {\bR }_2 \end{array}] \in {\mathcal R}^{r \times t}$](images/imlug_langref0192.png) is upper trapezoidal,
is upper trapezoidal, 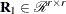 is upper triangular and invertible,
is upper triangular and invertible, 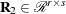 ,
, ![${\bQ } = [\begin{array}{cc} {\bY } & {\bZ } \end{array}]$](images/imlug_langref0195.png) is orthogonal,
is orthogonal, 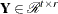 ,
, 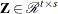 , and
, and 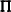 permutes the columns of
permutes the columns of 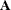 .
.
-
Use the transpose
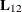 of the upper trapezoidal matrix
of the upper trapezoidal matrix ![${\bR } = \left[ \begin{array}{cc} {\bR }_1 & {\bR }_2 \end{array} \right]$](images/imlug_langref0200.png) ,
,
![\[ {\bL }_{12} = \left[ \begin{array}{c} {\bL }_1 \\ {\bL }_2 \end{array} \right] = {\bR }^{\prime } \in {\mathcal R}^{t \times r} \]](images/imlug_langref0201.png)
with
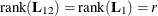 ,
, 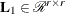 lower triangular,
lower triangular, 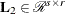 . The lower trapezoidal matrix
. The lower trapezoidal matrix 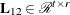 is premultiplied with
is premultiplied with  Householder transformations
Householder transformations 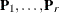 ,
,
![\[ \bP _ r \ldots \bP _1 \left[ \begin{array}{c} \bL _1 \\ \bL _2 \end{array} \right] = \left[ \begin{array}{c} \bL \\ \mb {0} \end{array} \right] \]](images/imlug_langref0207.png)
each zeroing out one of the
 columns of
columns of 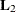 and producing the nonsingular lower triangular matrix
and producing the nonsingular lower triangular matrix 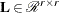 . Therefore, you obtain
. Therefore, you obtain
![\[ \bA = \bQ \left[ \begin{array}{cc} \bL ^{\prime } & \mb {0} \\ \mb {0} & \mb {0} \end{array} \right]\bPi ^{\prime } \bP ^{\prime } = \bY \left[ \begin{array}{cc} \bL ^{\prime } & \mb {0} \end{array} \right] \bPi ^{\prime } \bP ^{\prime } \]](images/imlug_langref0210.png)
with
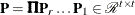 and upper triangular
and upper triangular 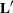 . This second step is described in Golub and Van Loan (1989).
. This second step is described in Golub and Van Loan (1989).
-
Compute the Moore-Penrose inverse
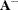 explicitly:
explicitly: ![\[ \bA ^- = \bP \bPi \left[ \begin{array}{cc} (\bL ^{\prime })^{-1} & \mb {0} \\ \mb {0} & \mb {0} \end{array} \right] \bQ ^{\prime } = \bP \bPi \left[ \begin{array}{c} (\bL ^{\prime })^{-1} \\ \mb {0} \end{array} \right] \bY ^{\prime } \]](images/imlug_langref0212.png)
-
Obtain
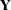 in
in ![${\bQ } = \left[\begin{array}{cc} {\bY } & {\bZ } \end{array}\right]$](images/imlug_langref0214.png) explicitly by applying the
explicitly by applying the  Householder transformations obtained in the first step to
Householder transformations obtained in the first step to ![$\left[ \begin{array}{c} {\bI }_ r \\ \mb {0} \end{array} \right]$](images/imlug_langref0215.png) .
.
-
Solve the
 lower triangular system
lower triangular system 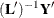 with
with  right-hand sides by using backward substitution, which yields an
right-hand sides by using backward substitution, which yields an 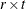 intermediate matrix.
intermediate matrix.
-
Left-apply the
 Householder transformations in
Householder transformations in 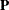 on the
on the 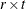 intermediate matrix
intermediate matrix ![$\left[ \begin{array}{c} ({\bL }^{\prime })^{-1}{\bY }^{\prime } \\ \mb {0} \\ \end{array} \right]$](images/imlug_langref0219.png) , which results in the symmetric matrix
, which results in the symmetric matrix 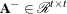 .
.
-
The GINV function computes the Moore-Penrose inverse ![]() by using the singular value decomposition of
by using the singular value decomposition of ![]() . Using complete orthogonal decomposition to compute
. Using complete orthogonal decomposition to compute ![]() usually requires far fewer floating-point operations. However, it can be slightly more sensitive to rounding errors, which
can disturb the detection of the true rank of
usually requires far fewer floating-point operations. However, it can be slightly more sensitive to rounding errors, which
can disturb the detection of the true rank of ![]() , than the singular value decomposition.
, than the singular value decomposition.
The following example demonstrates some uses of the COMPORT subroutine:
/* Only four linearly independent columns */
A = {1 0 1 0 0,
1 0 0 1 0,
1 0 0 0 1,
0 1 1 0 0,
0 1 0 1 0,
0 1 0 0 1 };
m = nrow(A);
n = ncol(A);
call comport(q,r,p,piv,lindep,A);
fullR = r // j(m-n, n, 0);
perm = i(n);
perm[piv,] = i(n);
/* recover A from factorization */
A2 = q*fullR*p`*perm`;
reset fuzz;
print A2;
/* compute Moore-Penrose generalized inverse */
rankA = n - lindep;
subR = R[1:rankA, 1:rankA];
fullRinv = j(n, n, 0);
fullRinv[1:rankA, 1:rankA] = inv(subR);
Ainv = perm*p*fullRinv*q[,1:n]`;
print Ainv;
/* verify generalized inverse */
eps = 1e-12;
if any(A*Ainv*A-A > eps) |
any(Ainv*A*Ainv-Ainv > eps) |
any((A*Ainv)`-A*Ainv > eps) |
any((Ainv*A)`-Ainv*A > eps) then
msg = "Pseudoinverse conditions not satisfied";
else
msg = "Pseudoinverse conditions satisfied";
print msg;
Figure 23.65: Results from a Complete Orthogonal Factorization
| A2 | ||||
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| Ainv | |||||
|---|---|---|---|---|---|
| 0.2666667 | 0.2666667 | 0.2666667 | -0.066667 | -0.066667 | -0.066667 |
| -0.066667 | -0.066667 | -0.066667 | 0.2666667 | 0.2666667 | 0.2666667 |
| 0.4 | -0.1 | -0.1 | 0.4 | -0.1 | -0.1 |
| -0.1 | 0.4 | -0.1 | -0.1 | 0.4 | -0.1 |
| -0.1 | -0.1 | 0.4 | -0.1 | -0.1 | 0.4 |
| msg |
|---|
| Pseudoinverse conditions satisfied |