ARMASIM Function :: SAS/IML(R) 12.3 User's Guide

ARMASIM Function

ARMASIM (phi, theta, mu, sigma, n <, seed> ) ;

The ARMASIM function simulates a univariate series from a autoregressive moving average (ARMA) model.

The arguments to the ARMASIM function are as follows:

phi

is a 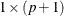$1 \times (p+1)$ matrix that contains the autoregressive parameters. The first element is assumed to have the value 1.

theta

is a 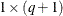$1 \times (q+1)$ matrix that contains the moving average parameters. The first element is assumed to have the value 1.

mu

is a scalar that contains the overall mean of the series.

sigma

is a scalar that contains the standard deviation of the innovation series.

n

is a scalar that contains , the length of the series. The value of must be greater than 0.

seed

is a scalar that contains the random number seed. At the first execution of the function, the seed variable is used as follows:

If seed > 0, the input seed is used for generating the series.
If seed = 0, the system clock is used to generate the seed.
If seed < 0, the value –seed is used for generating the series.

If the seed is not supplied, the system clock is used to generate the seed.

On subsequent calls to the function, the seed variable is used as follows:

If seed > 0, the seed remains unchanged.
In other cases, after each execution of the function, the current seed is updated internally.

The ARMASIM function generates a series of length from a given autoregressive moving average (ARMA) time series model and returns the series in an $n \times 1$ matrix. The notational conventions for the ARMASIM function are the same as those used by the ARMACOV subroutine. See the description of the ARMACOV call for the model employed. The ARMASIM function uses an exact simulation algorithm as described in Woodfield (1988). A sequence $Y_0,Y_1,\ldots ,Y_{p+q-1}$ of starting values is produced by using an expanded covariance matrix, and then the remaining values are generated by using the following recursion form of the model:

$Y_ t = -\sum _{i=1}^ p \phi _ i Y_{t-i} + \epsilon _ t + \sum _{i=1}^ q \theta _ i \epsilon _{t-i} ~ ~ ~ ~ ~ ~ t = p+q, ~ p+q+1,\ldots , ~ n-1$

The random number generator RANNOR is used to generate the noise component of the model. Note that the following statement returns standard normal pseudorandom deviates:

y = armasim(1, 1, 0, 1, n, seed);

For example, consider the following model:

$y_ t = 0.5y_{t-1} + e_ t + 0.8e_{t-1}$

To generate a time series of length 10 from this model, use the following statements to produce the result shown in Figure 23.47:

phi = {1 -0.5};
theta = {1 0.8};
y = armasim(phi, theta, 0, 1, 10, -1234321);
print y;

Figure 23.47: Simulated Time Series

y
2.3253578
0.975835
-0.376358
-0.878433
-2.515351
-3.083021
-1.996886
-1.839975
-0.214027
1.4786717