Overview
SAS/IML has four subroutines that can be used for outlier detection and robust regression. The Least Median of Squares (LMS) and Least Trimmed Squares (LTS) subroutines perform robust regression (sometimes called resistant regression). These subroutines are able to detect outliers and perform a least-squares regression on the remaining observations. The Minimum Volume Ellipsoid Estimation (MVE) and Minimum Covariance Determinant Estimation (MCD) subroutines can be used to find a robust location and a robust covariance matrix that can be used for constructing confidence regions, detecting multivariate outliers and leverage points, and conducting robust canonical correlation and principal component analysis.
The LMS, LTS, MVE, and MCD methods were developed by Rousseeuw (1984) and Rousseeuw and Leroy (1987). All of these methods have the high breakdown value property. Roughly speaking, the breakdown value is a measure of the proportion of contamination that a procedure can withstand and still maintain its robustness.
The algorithm used in the LMS subroutine is based on the PROGRESS program of Rousseeuw and Hubert (1996), which is an updated version of Rousseeuw and Leroy (1987). In the special case of regression through the origin with a single regressor, Barreto and Maharry (2006) show that the PROGRESS algorithm does not, in general, find the slope that yields the least median of squares. Starting with release 9.2, the LMS subroutine uses the algorithm of Barreto and Maharry (2006) to obtain the correct LMS slope in the case of regression through the origin with a single regressor. In this case, inputs to the LMS subroutine specific to the PROGRESS algorithm are ignored and output specific to the PROGRESS algorithm is suppressed.
The algorithm used in the LTS subroutine is based on the algorithm FAST-LTS of Rousseeuw and Van Driessen (2000). The MCD algorithm is based on the FAST-MCD algorithm given by Rousseeuw and Van Driessen (1999), which is similar to the FAST-LTS algorithm. The MVE algorithm is based on the algorithm used in the MINVOL program by Rousseeuw (1984). LTS estimation has higher statistical efficiency than LMS estimation. With the FAST-LTS algorithm, LTS is also faster than LMS for large data sets. Similarly, MCD is faster than MVE for large data sets.
Besides LTS estimation and LMS estimation, there are other methods for robust regression and outlier detection. You can refer to a comprehensive procedure, PROC ROBUSTREG, in SAS/STAT. A summary of these robust tools in SAS can be found in Chen (2002).
The four SAS/IML subroutines are designed for the following:
-
LMS: minimizing the
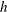 th ordered squared residual
th ordered squared residual
-
LTS: minimizing the sum of the
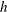 smallest squared residuals
smallest squared residuals
-
MCD: minimizing the determinant of the covariance of
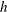 points
points
-
MVE: minimizing the volume of an ellipsoid that contains
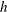 points
points
where ![]() is defined in the range
is defined in the range
|
|
In the preceding equation, ![]() is the number of observations and
is the number of observations and ![]() is the number of regressors.[1] The value of
is the number of regressors.[1] The value of ![]() determines the breakdown value, which is “the smallest fraction of contamination that can cause the estimator
determines the breakdown value, which is “the smallest fraction of contamination that can cause the estimator ![]() to take on values arbitrarily far from
to take on values arbitrarily far from ![]() ” (Rousseeuw and Leroy, 1987). Here,
” (Rousseeuw and Leroy, 1987). Here, ![]() denotes an estimator and
denotes an estimator and ![]() applies
applies ![]() to a sample
to a sample ![]() .
.
For each parameter vector ![]() , the residual of observation
, the residual of observation ![]() is
is ![]() . You then denote the ordered, squared residuals as
. You then denote the ordered, squared residuals as
|
|
The objective functions for the LMS, LTS, MCD, and MVE optimization problems are defined as follows:
-
LMS, the objective function for the LMS optimization problem is the
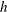 th ordered squared residual,
th ordered squared residual,
![\[ F_\mr {LMS} = (r^2)_{h:N} \longrightarrow \min \]](images/imlug_robustregexpls0012.png)
Note that, for
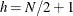 , the
, the 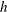 th quantile is the median of the squared residuals. The default
th quantile is the median of the squared residuals. The default 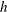 in PROGRESS is
in PROGRESS is ![$h = \left[ \frac{N+n+1}{2} \right]$](images/imlug_robustregexpls0014.png) , which yields the breakdown value (where
, which yields the breakdown value (where ![$[k]$](images/imlug_robustregexpls0015.png) denotes the integer part of
denotes the integer part of 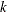 ).
).
-
LTS, the objective function for the LTS optimization problem is the sum of the
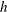 smallest ordered squared residuals,
smallest ordered squared residuals,
![\[ F_\mr {LTS} = \sqrt { \frac{1}{h} \sum _{i=1}^ h (r^2)_{i:N} } \longrightarrow \min \]](images/imlug_robustregexpls0017.png)
-
MCD, the objective function for the MCD optimization problem is based on the determinant of the covariance of the selected
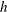 points,
points,
![\[ F_\mr {MCD} = \mbox{det}(\mb {C}_ h) \longrightarrow \min \]](images/imlug_robustregexpls0018.png)
where
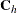 is the covariance matrix of the selected
is the covariance matrix of the selected 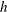 points.
points.
-
MVE, the objective function for the MVE optimization problem is based on the
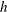 th quantile
th quantile 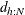 of the Mahalanobis-type distances
of the Mahalanobis-type distances 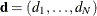 ,
,
![\[ F_\mr {MVE} = \sqrt {d_{h:N} \mbox{det}(\mb {C})} \longrightarrow \min \]](images/imlug_robustregexpls0022.png)
subject to
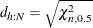 , where
, where  is the scatter matrix estimate, and the Mahalanobis-type distances are computed as
is the scatter matrix estimate, and the Mahalanobis-type distances are computed as
![\[ \mb {d} = \mbox{diag}(\sqrt { (\mb {X} - T)^ T \mb {C}^{-1} (\mb {X} - T)} ) \]](images/imlug_robustregexpls0025.png)
where
 is the location estimate.
is the location estimate.
Because of the nonsmooth form of these objective functions, the estimates cannot be obtained with traditional optimization
algorithms. For LMS and LTS, the algorithm, as in the PROGRESS program, selects a number of subsets of ![]() observations out of the
observations out of the ![]() given observations, evaluates the objective function, and saves the subset with the lowest objective function. As long as
the problem size enables you to evaluate all such subsets, the result is a global optimum. If computing time does not permit
you to evaluate all the different subsets, a random collection of subsets is evaluated. In such a case, you might not obtain
the global optimum.
given observations, evaluates the objective function, and saves the subset with the lowest objective function. As long as
the problem size enables you to evaluate all such subsets, the result is a global optimum. If computing time does not permit
you to evaluate all the different subsets, a random collection of subsets is evaluated. In such a case, you might not obtain
the global optimum.
Note that the LMS, LTS, MCD, and MVE subroutines are executed only when the number ![]() of observations is more than twice the number
of observations is more than twice the number ![]() of explanatory variables
of explanatory variables ![]() (including the intercept)—that is, if
(including the intercept)—that is, if ![]() .
.
[1] The value of ![]() can be specified, but in most applications the default value works just fine and the results seem to be quite stable with
different choices of
can be specified, but in most applications the default value works just fine and the results seem to be quite stable with
different choices of ![]() .
.