MAHALANOBIS Function
MAHALANOBIS (x, <, center> <, cov> ) ;
The MAHALANOBIS function returns the Mahalanobis distance between center and the rows of x, measured according to the Mahalanobis metric. The arguments are as follows:
- x
-
specifies an
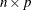 numerical matrix that contains
numerical matrix that contains  points in
points in 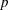 -dimensional space.
-dimensional space.
- center
-
is a
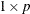 numerical vector that contains a point in
numerical vector that contains a point in 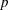 -dimensional space. The function returns the distances from the rows of x to center. If center is not specified, the sample mean,
-dimensional space. The function returns the distances from the rows of x to center. If center is not specified, the sample mean,  , is used.
, is used.
- cov
-
is an
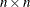 covariance matrix that specifies the metric that is used to compute distances. If cov is the identity matrix, then the function returns the usual Euclidean distance. If cov is not specified, the sample covariance matrix of x is used. In this case, the number of rows of x must be strictly greater than the number of columns, so that the covariance matrix is nonsingular.
covariance matrix that specifies the metric that is used to compute distances. If cov is the identity matrix, then the function returns the usual Euclidean distance. If cov is not specified, the sample covariance matrix of x is used. In this case, the number of rows of x must be strictly greater than the number of columns, so that the covariance matrix is nonsingular.
If ![]() and
and ![]() are
are ![]() -dimensional row vectors and
-dimensional row vectors and ![]() is a covariance matrix, then the Mahalanobis distance between
is a covariance matrix, then the Mahalanobis distance between ![]() and
and ![]() is
is
|
|
The following statements compute the Mahalanobis distance between the rows of x and the point ![]() :
:
x = {1 0,
0 1,
-1 0,
0 -1};
center = {1 1};
cov = {4 1,
1 9};
maha = mahalanobis(x, center, cov);
print maha;
Figure 24.3: Mahalanobis Distance between Pairs of Points
| maha |
|---|
| 0.3380617 |
| 0.5070926 |
| 1.0141851 |
| 0.7745967 |
When the cov argument is an identity matrix, the Mahalanobis distance simplifies to the usual Euclidean distance. See the DISTANCE function for more information.