RATIO Function :: SAS/IML(R) 12.1 User's Guide

RATIO Function

RATIO (ar, ma, terms <, dim> ) ;

The RATIO function divides matrix polynomials.

The arguments to the RATIO function are as follows:

ar: is an 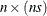$n \times (ns)$ matrix that represents a matrix polynomial generating function, 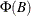$\Phi (B)$ , in the variable 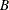. The first 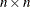$n \times n$ submatrix represents the constant term and must be nonsingular, the second 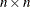$n \times n$ submatrix represents the first-order coefficients, and so on.
ma: is an 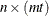$n \times (mt)$ matrix that represents a matrix polynomial generating function, 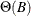$\Theta (B)$ , in the variable 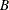. The first 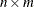$n \times m$ submatrix represents the constant term, the second 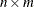$n \times m$ submatrix represents the first-order term, and so on.
terms: is a scalar that contains the number of terms to be computed, denoted by in the following discussion. This value must be positive.
dim: is a scalar that contains the value of 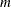, a dimension of the matrix ma. The default value is 1.

The RATIO function multiplies a matrix of polynomials by the inverse of another matrix of polynomials. It is useful for expressing univariate and multivariate ARMA models in pure moving average or pure autoregressive forms.

The value returned is an $n \times (mr)$ matrix that contains the terms of $\Phi (B)^{-1} \Theta (B)$ considered as a matrix of rational functions in that have been expanded as power series.

The RATIO function can be used to consolidate the matrix operators that are used in a multivariate time series model of the form

$\Phi (B) \mb {Y}_ t = \Theta (B) \epsilon _ t$

where $\Phi (B)$ and $\Theta (B)$ are matrix polynomial operators whose first matrix coefficients are identity matrices. The RATIO function can be used to compute a truncated form of $\Psi (B) = \Phi (B)^{-1} \Theta (B)$ for the equivalent infinite-order model

$\mb {Y}_ t = \Psi (B) \epsilon _ t$

The RATIO function can also be used for simple scalar polynomial division, giving a truncated form of $\theta (x)/\phi (x)$ for two scalar polynomials $\theta (x)$ and $\phi (x)$ .

The cumulative sum of the elements of a column vector x can be obtained by using the following statement:

 ratio({ 1 -1}, x, ncol(x));

The following example defines polynomial coefficients that are used in a multivariate ARMA(1,1) model and computes the ratio of the polynomials:

ar = {1 0 -0.5  2,
      0 1  3   -0.8};
ma = {1 0  0.9  0.7,
      0 1  2   -0.4};
psi = ratio(ar, ma, 4, 2);
print psi;

Figure 23.275: The Ratio of Polynomials

psi
1	0	1.4	-1.3	2.7	-1.45	11.35	-9.165
0	1	-1	0.4	-5	4.22	-12.1	7.726