KALDFF Call :: SAS/IML(R) 12.1 User's Guide

KALDFF Call

CALL KALDFF (pred, vpred, initial, s2, data, lead, int, coef, var, intd, coefd <*>, n0 <*>, at <*>, mt <*>, qt ) ;

The KALDFF subroutine computes the one-step forecast of state vectors in an SSM by using the diffuse Kalman filter. The call estimates the conditional expectation of , and also estimates the initial random vector, $\delta$ , and its covariance matrix.

The input arguments to the KALDFF subroutine are as follows:

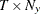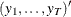data: is a $T \times N_ y$ matrix that contains data $(y_1, \ldots , y_ T)^{\prime }$ .
lead: is the number of steps to forecast after the end of the data set.
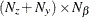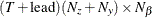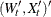int: is an $(N_ z + N_ y) \times N_\beta$ matrix for a time-invariant fixed matrix, or a $(T+\mbox{lead})(N_ z + N_ y) \times N_\beta$ matrix that contains fixed matrices for the time-variant model in the transition equation and the measurement equation—that is, $(W^{\prime }_ t, X^{\prime }_ t)^{\prime }$ .
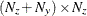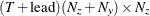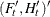coef: is an $(N_ z + N_ y) \times N_ z$ matrix for a time-invariant coefficient, or a $(T+\mbox{lead})(N_ z + N_ y) \times N_ z$ matrix that contains coefficients at each time in the transition equation and the measurement equation—that is, $(F^{\prime }_ t, H^{\prime }_ t)^{\prime }$ .
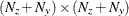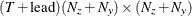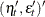var: is an $(N_ z + N_ y) \times (N_ z + N_ y)$ matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation, or a $(T+\mbox{lead})(N_ z + N_ y) \times (N_ z + N_ y)$ matrix that contains covariance matrices for the error in the transition equation and the error in the measurement equation—that is, $(\eta ^{\prime }_ t, \epsilon ^{\prime }_ t)^{\prime }$ .
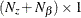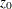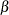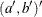intd: is an $(N_ z + N_\beta ) \times 1$ vector that contains the intercept term in the equation for the initial state vector and the mean effect $\beta$ —that is, $(a^{\prime }, b^{\prime })^{\prime }$ .
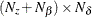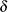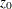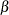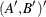coefd: is an $(N_ z + N_\beta ) \times N_\delta$ matrix that contains coefficients for the initial state $\delta$ in the equation for the initial state vector and the mean effect $\beta$ —that is, $(A^{\prime }, B^{\prime })^{\prime }$ .
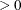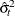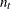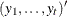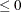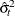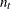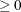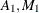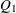n0: is an optional scalar including an initial denominator. If n0, the denominator for $\hat{\sigma }^2_ t$ is n0 plus the number of elements of $(y_1, \ldots , y_ t)^{\prime }$ . If n0 $\leq 0$ or n0 is not specified, the denominator for $\hat{\sigma }^2_ t$ is . With n0 $\geq 0$ , the initial values, , and , are assumed to be known and, hence, at, mt, and qt are used for input that contains the initial values. If the value of n0 is negative or n0 is not specified, the initial values for at, mt, and qt are computed. The value of n0 is updated as 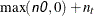$\max (\mbox{\Argument{n0}},0) + n_ t$ after the KALDFF call.
at: is an optional 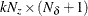$kN_ z \times (N_\delta + 1)$ matrix. If n0 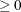$\geq 0$ , at contains 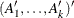$(A^{\prime }_1, \ldots , A^{\prime }_ k)^{\prime }$ . However, only the first matrix 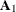$\mathbf{A}_1$ is used as input. When you specify the KALDFF call, at returns 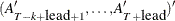$(A^{\prime }_{T-k+\mbox{lead}+1}, \ldots , A^{\prime }_{T+\mbox{lead}})^{\prime }$ . If n0 is negative or the matrix 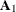$\mathbf{A}_1$ contains missing values, 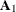$\mathbf{A}_1$ is automatically computed.
mt: is an optional 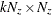$kN_ z \times N_ z$ matrix. If n0 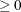$\geq 0$ , mt contains 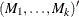$(M_1, \ldots , M_ k)^{\prime }$ . However, only the first matrix 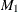is used as input. If n0 is negative or the matrix 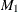contains missing values, mt is used for output, and it contains 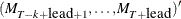$(M_{T-k+\mbox{lead}+1}, \ldots , M_{T+\mbox{lead}})^{\prime }$ . Note that the matrix 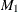can be used as an input matrix if either of the off-diagonal elements is not missing. The missing element 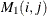is replaced by the nonmissing element .
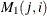qt: is an optional 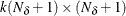$k(N_\delta + 1) \times (N_\delta + 1)$ matrix. If n0 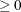$\geq 0$ , qt contains 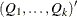$(Q_1, \ldots , Q_ k)^{\prime }$ . However, only the first matrix 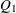is used as input. If n0 is negative or the matrix 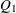contains missing values, qt is used for output and contains 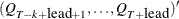$(Q_{T-k+\mbox{lead}+1}, \ldots , Q_{T+\mbox{lead}})^{\prime }$ . The matrix 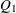can also be used as an input matrix if either of the off-diagonal elements is not missing since the missing element 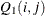is replaced by the nonmissing element .

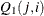The KALDFF call returns the following values:

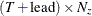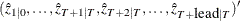pred: is a $(T+\mbox{lead}) \times N_ z$ matrix that contains estimated predicted state vectors $(\hat{z}_{1|0}, \ldots , \hat{z}_{T+1|T}, \hat{z}_{T+2|T}, \ldots , \hat{z}_{T+\mbox{lead}|T})^{\prime }$ .
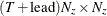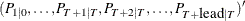vpred: is a $(T+\mbox{lead})N_ z \times N_ z$ matrix that contains estimated mean square errors of predicted state vectors $(P_{1|0}, \ldots , P_{T+1|T}, P_{T+2|T}, \ldots , P_{T+\mbox{lead}|T})^{\prime }$ .
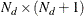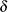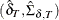initial: is an $N_ d \times (N_ d + 1)$ matrix that contains an estimate and its variance for initial state $\delta$ , that is, $(\hat{\delta }_ T, \hat{\Sigma }_{\delta , T})$ .
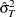s2: is a scalar that contains the estimated variance $\hat{\sigma }^2_ T$ .

The KALDFF call computes the one-step forecast of state vectors in an SSM by using the diffuse Kalman filter. The SSM for the diffuse Kalman filter is written

$\displaystyle y_ t$	$\displaystyle =$	$\displaystyle X_ t \beta + H_ t z_ t + \epsilon _ t$
$\displaystyle z_{t+1}$	$\displaystyle =$	$\displaystyle W_ t \beta + F_ t z_ t + \eta _ t$
$\displaystyle z_0$	$\displaystyle =$	$\displaystyle a + A \delta$
$\displaystyle \beta$	$\displaystyle =$	$\displaystyle b + B \delta$

where is an $N_ z \times 1$ state vector, is an $N_ y \times 1$ observed vector, and

$\displaystyle \left[ \begin{array}{c} \eta _ t \\ \epsilon _ t \end{array} \right]$	$\displaystyle \sim$	$\displaystyle N \left(\mb {0}, \sigma ^2 \left[ \begin{array}{cc} V_ t & G_ t \\ G^{\prime }_ t & R_ t \end{array} \right] \right)$
$\displaystyle \delta$	$\displaystyle \sim$	$\displaystyle N(\mu , \sigma ^2\Sigma )$

It is assumed that the noise vector $(\eta ^{\prime }_ t, \epsilon ^{\prime }_ t)^{\prime }$ is independent and $\delta$ is independent of the vector $(\eta ^{\prime }_ t, \epsilon ^{\prime }_ t)^{\prime }$ . The matrices, , , , , , , , , , , and , are assumed to be known. The KALDFF call estimates the conditional expectation of the state vector given the observations. The KALDFF subroutine also produces the estimates of the initial random vector $\delta$ and its covariance matrix. For -step forecasting where , the estimated conditional expectation at time is computed with observations given up to time . The estimated -step forecast and its estimated MSE are denoted $z_{t+k|t}$ and $P_{t+k|t}$ (for ). $A_{t+k(\delta )}$ and $E_{t(\delta )}$ are last-column-deleted submatrices of $A_{t+k}$ and , respectively. The algorithm for one-step prediction is given as follows:

$\displaystyle E_ t$	$\displaystyle =$	$\displaystyle (X_ t B, ~ y_ t - X_ t b) - H_ t A_ t$
$\displaystyle D_ t$	$\displaystyle =$	$\displaystyle H_ t M_ t H^{\prime }_ t + R_ t$
$\displaystyle Q_{t+1}$	$\displaystyle =$	$\displaystyle Q_ t + E^{\prime }_ t D_ t^- E_ t$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[\begin{array}{cc} S_ t & s_ t \\ s^{\prime }_ t & q_ t \end{array} \right]$
$\displaystyle \hat{\sigma }^2_ t$	$\displaystyle =$	$\displaystyle (q_ t - s^{\prime }_ t S_ t^- s_ t)/n_ t$
$\displaystyle \hat{\delta }_ t$	$\displaystyle =$	$\displaystyle S^-_ t s_ t$
$\displaystyle \hat{\Sigma }_{\delta ,t}$	$\displaystyle =$	$\displaystyle \hat{\sigma }^2_ t S^-_ t$
$\displaystyle K_ t$	$\displaystyle =$	$\displaystyle (F_ t M_ t H^{\prime }_ t + G_ t)D^-_ t$
$\displaystyle A_{t+1}$	$\displaystyle =$	$\displaystyle W_ t(-B, b) + F_ t A_ t + K_ tE_ t$
$\displaystyle M_{t+1}$	$\displaystyle =$	$\displaystyle (F_ t - K_ t H_ t) M_ t F^{\prime }_ t + V_ t - K_ t G^{\prime }_ t$
$\displaystyle z_{t+1\|t}$	$\displaystyle =$	$\displaystyle A_{t+1}(-\hat{\delta }^{\prime }_ t, 1)^{\prime }$
$\displaystyle P_{t+1\|t}$	$\displaystyle =$	$\displaystyle \hat{\sigma }^2_ t \bM _{t+1} + A_{t+1(\delta )} \hat{\Sigma }_{\delta ,t} A^{\prime }_{t+1(\delta )}$

where is the number of elements of $(y_1,\ldots ,y_ t)^{\prime }$ plus $\max (\mbox{\Argument{n0}},0)$ . Unless initial values are given and n0 $\geq 0$ , initial values are set as follows:

$\displaystyle A_1$	$\displaystyle =$	$\displaystyle W_1(-B,b) + F_1(-A,a)$
$\displaystyle M_1$	$\displaystyle =$	$\displaystyle V_1$
$\displaystyle Q_1$	$\displaystyle =$	$\displaystyle \mb {0}$

For -step forecasting where ,

$\displaystyle A_{t+k}$	$\displaystyle =$	$\displaystyle W_{t+k-1}(-B,b) + F_{t+k-1} A_{t+k-1}$
$\displaystyle M_{t+k}$	$\displaystyle =$	$\displaystyle F_{t+k-1} M_{t+k-1} F^{\prime }_{t+k-1} + V_{t+k-1}$
$\displaystyle D_{t+k}$	$\displaystyle =$	$\displaystyle H_{t+k} M_{t+k} H^{\prime }_{t+k} + R_{t+k}$
$\displaystyle z_{t+k\|t}$	$\displaystyle =$	$\displaystyle A_{t+k}(-\hat{\delta }^{\prime }_ t,1)^{\prime }$
$\displaystyle P_{t+k\|t}$	$\displaystyle =$	$\displaystyle \hat{\sigma }^2_ t M_{t+k} + A_{t+k(\delta )} \hat{\Sigma }_{\delta ,t} A^{\prime }_{t+k(\delta )}$

If there is a missing observation, the KALDFF call computes the one-step forecast for the observation that follows the missing observation as the two-step forecast from the previous observation.

An example that uses the KALDFF call is in the documentation for the KALDFS call.