INVUPDT Function
INVUPDT (matrix, vector<, scalar>) ;
The INVUPDT function updates a matrix inverse.
The arguments to the INVUPDT function are as follows:
- matrix
-
is an
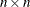 nonsingular matrix. In most applications matrix is symmetric positive definite.
nonsingular matrix. In most applications matrix is symmetric positive definite.
- vector
-
is an
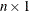 or
or 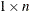 vector.
vector.
- scalar
-
is a numeric scalar.
The Sherman-Morrison-Woodbury formula is
|
|
where ![]() is an
is an ![]() nonsingular matrix and
nonsingular matrix and ![]() and
and ![]() are
are ![]() . The formula shows that a rank
. The formula shows that a rank ![]() update to
update to ![]() corresponds to a rank
corresponds to a rank ![]() update of
update of ![]() .
.
The INVUPDT function implements the Sherman-Morrison-Woodbury formula for rank-one updates with ![]() and
and ![]() , where
, where ![]() is an
is an ![]() vector and
vector and ![]() is a scalar.
is a scalar.
If ![]() , then you can call the INVUPDT function as follows:
, then you can call the INVUPDT function as follows:
R = invupdt(M, X, w);
This statement computes the following matrix:
|
|
The matrix ![]() is equivalent to
is equivalent to ![]() . If
. If ![]() is symmetric positive definite, then so is
is symmetric positive definite, then so is ![]() .
.
If ![]() is not specified, then it is given a default value of
is not specified, then it is given a default value of ![]() .
.
A common use of the INVUPDT function is in linear regression. If ![]() is a design matrix,
is a design matrix, ![]() is the associated inverse crossproduct matrix, and
is the associated inverse crossproduct matrix, and ![]() is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that
includes the new observation can be updated from
is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that
includes the new observation can be updated from ![]() by using the following statement:
by using the following statement:
M2 = invupdt(M, v);
If ![]() is
is ![]() , the function adds an observation to the inverse; if
, the function adds an observation to the inverse; if ![]() is
is ![]() , the function removes an observation from the inverse. If weighting is used,
, the function removes an observation from the inverse. If weighting is used, ![]() is the weight.
is the weight.
To perform the computation, the INVUPDT function uses about ![]() multiplications and additions, where
multiplications and additions, where ![]() is the row dimension of the positive definite argument matrix.
is the row dimension of the positive definite argument matrix.
The following program demonstrates adding or removing observations from a linear fit and updating the inverse crossproduct matrix:
X = {0, 1, 1, 1, 2, 2, 3, 4, 4};
Y = {1, 1, 2, 6, 2, 3, 3, 3, 4};
/* find linear fit */
Z = j(nrow(X), 1, 1) || X; /* design matrix */
M = inv(Z`*Z);
b = M*Z`*Y; /* LS estimate */
resid = Y - Z*b; /* residuals */
print "Original Fit", b resid;
/* residual for observation (1,6) seems too large.
Take obs number 4 out of data set and refit. */
v = z[4,];
M = invupdt(M, v, -1); /* update inverse crossprod */
keepObs = (1:3) || (5:nrow(X));
Z = Z[keepObs, ];
Y = Y[keepObs, ];
b = M*Z`*Y; /* new LS estimate */
print "After deleting observation 4", b;
/* Add a new obs (x,y) = (0,2) and refit. */
obs = {0 2};
v = 1 || obs[1]; /* new row in design matrix */
M = invupdt(M, v);
Z = Z // v;
Y = Y // obs[2];
b = M*Z`*Y; /* new LS estimate */
print "After adding observation (0,2)", b;
Figure 23.148: Refitting Linear Regression Models
| Original Fit |
| b | resid |
|---|---|
| 2.0277778 | -1.027778 |
| 0.375 | -1.402778 |
| -0.402778 | |
| 3.5972222 | |
| -0.777778 | |
| 0.2222222 | |
| -0.152778 | |
| -0.527778 | |
| 0.4722222 |
| After deleting observation 4 |
| b |
|---|
| 1 |
| 0.6470588 |
| After adding observation (0,2) |
| b |
|---|
| 1.3 |
| 0.5470588 |