FARMAFIT Call
CALL FARMAFIT (d, phi, theta, sigma, series <*>, p <*>, q <*>, opt ) ;
The FARMAFIT subroutine estimates the parameters of an ARFIMA(![]() ) model.
) model.
The input arguments to the FARMAFIT subroutine are as follows:
- series
-
specifies a time series (assuming mean zero).
- p
-
specifies the set or subset of the AR order. If you do not specify p, the default is p
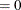 .
.
If you specify p=3, the FARMAFIT subroutine estimates the coefficient of the lagged variable
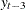 .
.
If you specify p=
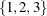 , the FARMAFIT subroutine estimates the coefficients of lagged variables
, the FARMAFIT subroutine estimates the coefficients of lagged variables 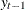 ,
, 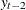 , and
, and 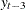 .
.
- q
-
specifies the subset of the MA order. If you do not specify q, the default value is 0.
If you specify q=2, the FARMAFIT subroutine estimates the coefficient of the lagged variable
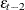 .
.
If you specify q=
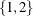 , the FARMAFIT subroutine estimates the coefficients of lagged variables
, the FARMAFIT subroutine estimates the coefficients of lagged variables 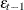 and
and 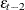 .
.
- opt
-
specifies the method of computing the log-likelihood function.
- 0
-
requests the conditional sum of squares function. This is the default.
- 1
-
requests the exact log-likelihood function. This option requires that the time series be stationary and invertible.
The FARMAFIT subroutine returns the following values:
- d
-
is a scalar that contains a fractional differencing order.
- phi
-
is a vector that contains the autoregressive coefficients.
- theta
-
is a vector that contains the moving average coefficients.
- sigma
-
is a scalar that contains a variance of the innovation series.
As an example, consider the following ARFIMA(![]() ) model:
) model:
|
|
In this model, ![]() . The following statements estimate the parameters of this model:
. The following statements estimate the parameters of this model:
d = 0.3; phi = 0.5; theta = -0.1; call farmasim(yt, d, phi, theta) seed=1234; call farmafit(d, ar, ma, sigma, yt) p=1 q=1; print d ar ma sigma;
Figure 23.114: Parameter Estimates for a ARFIMA Model
| d | ar | ma | sigma |
|---|---|---|---|
| 0.3950157 | 0.5676217 | -0.012339 | 1.2992989 |
The FARMAFIT subroutine estimates the parameters ![]() ,
, ![]() ,
, ![]() , and
, and ![]() of an ARFIMA(
of an ARFIMA(![]() ) model. The log-likelihood function is solved by iterative numerical procedures such as the quasi-Newton optimization. The
starting value
) model. The log-likelihood function is solved by iterative numerical procedures such as the quasi-Newton optimization. The
starting value ![]() is obtained by the approach of Geweke and Porter-Hudak (1983); the starting values of the AR and MA parameters are obtained from the least squares estimates.
is obtained by the approach of Geweke and Porter-Hudak (1983); the starting values of the AR and MA parameters are obtained from the least squares estimates.