A Module for Linear Regression
The linear systems that arise naturally in statistics are usually overconstrained, meaning that the 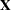 matrix has more rows than columns and that an exact solution to the linear system is impossible to find. Instead, the statistician assumes a linear model of the form
matrix has more rows than columns and that an exact solution to the linear system is impossible to find. Instead, the statistician assumes a linear model of the form
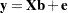 |
where 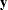 is the vector of responses,
is the vector of responses, 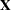 is a design matrix, and
is a design matrix, and 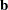 is a vector of unknown parameters that are estimated by minimizing the sum of squares of
is a vector of unknown parameters that are estimated by minimizing the sum of squares of  , the error or residual term.
, the error or residual term.
The following example illustrates some programming techniques by using SAS/IML statements to perform linear regression. (The example module does not replace regression procedures such as the REG procedure, which are more efficient for regressions and offer a multitude of diagnostic options.)
Suppose you have response data 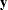 measured at five values of the independent variable
measured at five values of the independent variable 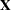 and you want to perform a quadratic regression. In this case, you can define the design matrix
and you want to perform a quadratic regression. In this case, you can define the design matrix 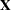 and the data vector
and the data vector 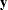 as follows:
as follows:
proc iml;
x = {1 1 1,
1 2 4,
1 3 9,
1 4 16,
1 5 25};
y = {1, 5, 9, 23, 36};
You can compute the least squares estimate of 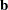 by using the following statement:
by using the following statement:
b = inv(x`*x) * x`*y; print b;
| b |
|---|
| 2.4 |
| -3.2 |
| 2 |
The predicted values are found by multiplying the data matrix and the parameter estimates; the residuals are the differences between actual and predicted responses, as shown in the following statements:
yhat = x*b; r = y-yhat; print yhat r;
| yhat | r |
|---|---|
| 1.2 | -0.2 |
| 4 | 1 |
| 10.8 | -1.8 |
| 21.6 | 1.4 |
| 36.4 | -0.4 |
To estimate the variance of the responses, calculate the sum of squared errors (SSE), the error degrees of freedom (DFE), and the mean squared error (MSE) as follows:
sse = ssq(r); dfe = nrow(x)-ncol(x); mse = sse/dfe; print sse dfe mse;
| sse | dfe | mse |
|---|---|---|
| 6.4 | 2 | 3.2 |
Notice that in computing the degrees of freedom, you use the function NCOL to return the number of columns of 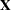 and the function NROW to return the number of rows.
and the function NROW to return the number of rows.
Now suppose you want to solve the problem repeatedly on new data. To do this, you can define a module. Modules begin with a START statement and end with a FINISH statement, with the program statements in between. The following statements define a module named Regress to perform linear regression:
start Regress; /* begins module */ xpxi = inv(x`*x); /* inverse of X'X */ beta = xpxi * (x`*y); /* parameter estimate */ yhat = x*beta; /* predicted values */ resid = y-yhat; /* residuals */ sse = ssq(resid); /* SSE */ n = nrow(x); /* sample size */ dfe = nrow(x)-ncol(x); /* error DF */ mse = sse/dfe; /* MSE */ cssy = ssq(y-sum(y)/n); /* corrected total SS */ rsquare = (cssy-sse)/cssy; /* RSQUARE */ print ,"Regression Results", sse dfe mse rsquare; stdb = sqrt(vecdiag(xpxi)*mse); /* std of estimates */ t = beta/stdb; /* parameter t tests */ prob = 1-probf(t#t,1,dfe); /* p-values */ print ,"Parameter Estimates",, beta stdb t prob; print ,y yhat resid; finish Regress; /* ends module */
Assuming that the matrices x and y are defined, you can run the Regress module as follows:
run Regress; /* executes module */
| Regression Results |
| sse | dfe | mse | rsquare |
|---|---|---|---|
| 6.4 | 2 | 3.2 | 0.9923518 |
| Parameter Estimates |
| beta | stdb | t | prob |
|---|---|---|---|
| 2.4 | 3.8366652 | 0.6255432 | 0.5954801 |
| -3.2 | 2.923794 | -1.094468 | 0.387969 |
| 2 | 0.4780914 | 4.1833001 | 0.0526691 |
| y | yhat | resid |
|---|---|---|
| 1 | 1.2 | -0.2 |
| 5 | 4 | 1 |
| 9 | 10.8 | -1.8 |
| 23 | 21.6 | 1.4 |
| 36 | 36.4 | -0.4 |