generates a random sample from a Dirichlet distribution

The inputs are as follows:

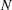
is the number of desired observations sampled from the distribution.

Shape

is a 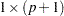vector of shape parameters for the distribution, .

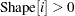The Dirichlet distribution is a multivariate generalization of the beta distribution. The RANDDIRICHLET function returns an 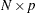matrix that contains 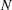random draws from the Dirichlet distribution.

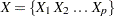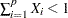If with and 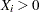follows a Dirichlet distribution with shape parameter 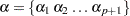, then

• the probability density function for is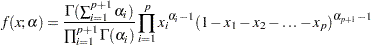

• if 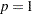, the probability distribution is a beta distribution.

• if 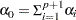, then

  • the expected value of 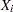is .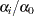

  • the variance of 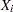is .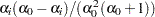

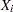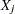  • the covariance of and is .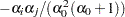

The following example generates 1000 samples from a two-dimensional Dirichlet distribution. Each row of the returned matrix x is a row vector sampled from the Dirichlet distribution. The example then computes the sample mean and covariance and compares them with the expected values. Here are the code and the output:

   call randseed(1);
   n = 1000;
   Shape = {2, 1, 1};
   x = RANDDIRICHLET(n,Shape);
   Shape0 = sum(Shape);
   d = nrow(Shape)-1;
   s = Shape[1:d];
   Mean = s`/Shape0;
   Cov = -s*s` / (Shape0##2*(Shape0+1));
   /* replace diagonal elements with variance */
   Variance = s#(Shape0-s) / (Shape0##2*(Shape0+1));
   do i = 1 to d;
      Cov[i,i] = Variance[i];
   end;

   SampleMean = x[:,];
   n = nrow(x);                    
   y = x - repeat( SampleMean, n );
   SampleCov = y`*y / (n-1);
   print SampleMean Mean, SampleCov Cov;

               SampleMean                Mean

           0.4992449 0.2485677       0.5      0.25

                SampleCov                 Cov

           0.0502652 -0.026085      0.05    -0.025
           -0.026085 0.0393922    -0.025    0.0375

For further details about sampling from the Dirichlet distribution, see Kotz, Balakrishnan, and Johnson (2000); Gentle (2003); or Devroye (1986).