Language Reference: VARMALIK Call

VARMALIK Call

CALL VARMALIK( lnl, series, phi, theta, sigma <*>, p <*>, q <*>, opt ) ;

The VARMALIK subroutine computes the log-likelihood function for a VARMA(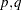 $\text{[math]}$ ) model.

The input arguments to the VARMALIK subroutine are as follows:

series

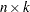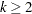specifies an $\text{[math]}$ matrix that contains the vector time series (assuming mean zero), where $\text{[math]}$ is the number of observations and $\text{[math]}$ is the number of variables.

phi

specifies a 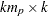$\text{[math]}$ matrix that contains the autoregressive coefficient matrices, where 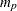$\text{[math]}$ is the number of the elements in the subset of the AR order. You must specify either phi or theta.

theta

specifies a 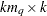$\text{[math]}$ matrix that contains the moving average coefficient matrices, where 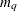$\text{[math]}$ is the number of the elements in the subset of the MA order. You must specify either phi or theta.

sigma

specifies a 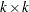$\text{[math]}$ covariance matrix of the innovation series. If you do not specify sigma, an identity matrix is used.

p

specifies the subset of the AR order. See the VARMACOV subroutine.

q

specifies the subset of the MA order. See the VARMACOV subroutine.

opt

specifies the method of computing the log-likelihood function:

opt=0: requests the multivariate innovations algorithm. This algorithm requires that the time series is stationary and does not contain missing observations.
opt=1: requests the conditional log-likelihood function. This algorithm requires that the number of the observations in the time series must be greater than p 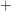$\text{[math]}$ q and that the series does not contain missing observations.
opt=2: requests the Kalman filtering algorithm. This is the default and is used if the required conditions in opt=0 and opt=1 are not satisfied.

The VARMALIK subroutine returns the following value:

lnl: is a $\text{[math]}$ matrix that contains the log-likelihood function, the sum of log determinant of the innovation variance, and the weighted sum of squares of residuals. The log-likelihood function is computed as $\text{[math]}$ (the sum of last two terms).

The options opt=0 and opt=2 are equivalent for stationary time series without missing values. Setting opt=0 is useful for a small number of the observations and a high order of p and q; opt=1 is useful for a high order of P and q; opt=2 is useful for a low order of p and q, or for missing values in the observations.

Consider the following bivariate (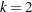 $\text{[math]}$ ) VARMA(1,1) model:

$\text{[math]}$

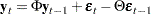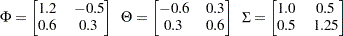To compute the log-likelihood function of this model, you can use the following statements:

  phi  = { 1.2 -0.5, 0.6 0.3 };
  theta= {-0.6  0.3, 0.3 0.6 };
  sigma= { 1.0  0.5, 0.5 1.25};
  call varmasim(yt, phi, theta) sigma=sigma;
  call varmalik(lnl, yt, phi, theta, sigma);