The TSPLINE subroutine fits a thin-plate smoothing spline (TPSS) to data. The generalized cross validation (GCV) function is used to select the smoothing parameter.

The TPSPLINE subroutine returns the following values:

fitted

is an 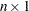vector of fitted values of the TPSS fit evaluated at the design points . The is the number of observations. The final TPSS fit depends on the optional lambda.

coeff

is a vector of spline coefficients. The vector contains the coefficients for basis functions in the null space and the representer of evaluation functions at unique design points. (see Wahba (1990) for more detail on reproducing kernel Hilbert space and representer of evaluation functions.) The length of coeff vector depends on the number of unique design points and the number of variables in the spline model. In general, let nuobs and 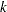be the number of unique rows and the number of columns of respectively. The length of coeff equals to 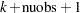. The coeff vector can be used as an input of TPSPLNEV to evaluate the resulting TPSS fit at new data points.

adiag

is an 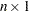vector of diagonal elements of the "hat" matrix. See the "Details" section.

gcv

If lambda is not specified, then gcv is the minimum value of the GCV function. If lambda is specified, then gcv is a vector (or scalar if lambda is a scalar) of GCV values evaluated at the lambda points. It provides you with both the ability to study the GCV curves by plotting gcv against lambda and the chance to identify a possible local minimum.

The input arguments to the TPSPLINE subroutine are as follows:

x

is an 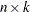matrix of design points on which the TPSS is to be fit. The 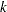is the number of variables in the spline model. The columns of need to be linearly independent and contain no constant column.

y

is the 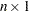vector of observations.

lambda

is a optional 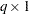vector that contains 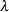values in 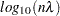scale. This option gives you the power to control how you want the TPSPLINE subroutine to function. If lambda is not specified (or lambda is specified and 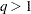) the GCV function is used to choose the "best" 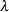and the returning fitted values are based on the 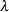that minimizes the GCV function. If lambda is specified and 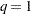, no minimization of the GCV function is involved and the fitted, coeff and adiag values are all based on the TPSS fit that uses this particular lambda. This gives you the freedom to choose the 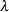that you deem appropriate.

Aside from the values returned, the TPSPLINE subroutine also prints other useful information such as the number of unique observations, the dimensions of the null space, the number of parameters in the model, a GCV estimate of 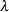, the smoothing penalty, the residual sum of square, the trace of 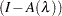, an estimate of 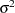, and the sum of squares for replication.

No missing values are accepted within the input arguments. Also, you should use caution if you want to specify small lambda values. Since the true 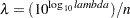, a very small value for lambda can cause 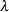to be smaller than the magnitude of machine error and usually the returned gcv values from such a 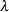cannot be trusted. Finally, when using TPSPLINE be aware that TPSS is a computationally intensive method. Therefore a large data set (that is, a large number of unique design points) will take a lot of computer memory and time.

For convenience, the TPSS method is illustrated with a two-dimensional independent variable . More details can be found in Wahba (1990), or in Bates et al. (1987).

Assume that the data are from the model

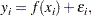where 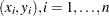are the observations. The function 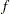is unknown and you assume that it is reasonably smooth. The error terms 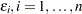are independent zero-mean random variables.

You measure the smoothness of 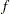by the integral over the entire plane of the square of the partial derivatives of 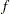of total order 2, that is

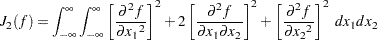Using this as a smoothness penalty, the thin-plate smoothing spline estimate 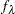of 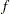is the minimizer of

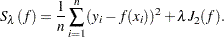Duchon (1976) derived that the minimizer 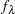can be represented as

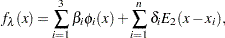where 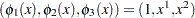and .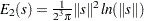

Let matrix 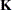have entries 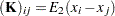and matrix 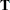have entries 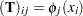. Then the minimization problem can be rewritten as finding coefficients 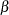and 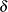to minimize

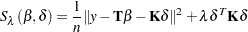The final TPSS fits can be viewed as a type of generalized ridge regression estimator. The 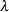is called the smoothing parameter, which controls the balance between the goodness of fit and the smoothness of the final estimate. The smoothing parameter can be chosen by minimizing the generalized cross validation function (GCV). If you write

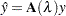and call the 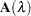as the "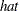" matrix, the GCV function 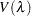is defined as

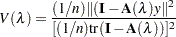The returned values from this function call provide the 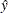as fitted, the 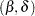as coeff, and 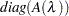as adiag.

To evaluate the TPSS fit 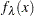at new data points, you can use the TPSPLNEV call.

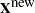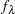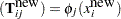Suppose , a matrix, contains the new data points at which you want to evaluate . Let and 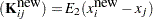be the 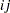th elements of 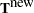and 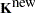respectively. The prediction at new data point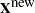s is

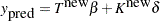Therefore, the 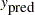can be easily evaluated by using the coefficient 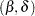obtained from the TPSPLINE call.

An example is given in the documentation for the TPSPLNEV call.