| ROOT Function |
ROOT(
matrix )
;
The ROOT function performs the Cholesky decomposition of a symmetric and positive definite matrix, 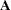 . The Cholesky decomposition factors
. The Cholesky decomposition factors  into the product
into the product
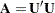 |
where 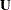 is upper triangular.
is upper triangular.
For example, the following statements compute the upper-triangular matrix, U, in the Cholesky decomposition of a matrix:
A = {25 0 5,
0 4 6,
5 6 59};
U = root(A);
print U;
Figure 23.268
Cholesky Decomposition
| U | ||
|---|---|---|
| 5 | 0 | 1 |
| 0 | 2 | 3 |
| 0 | 0 | 7 |
If you need to solve a linear system and you already have a Cholesky decomposition of your matrix, then use the TRISOLV function as illustrated by the following statements:
b = {5, 2, 53};
/* Want to solve A * v = b.
First solve U` z = b,
then solve U v = z */
z = trisolv(2, U, b);
v = trisolv(1, U, z);
print v;
Figure 23.269
Solution to a Linear System
| v |
|---|
| 0 |
| -1 |
| 1 |
The ROOT function performs most of its computations in the memory allocated for returning the Cholesky decomposition.