| PRODUCT Function |
The PRODUCT function multiplies matrices of polynomials.
The arguments to the PRODUCT function are as follows:
- a
is an
 numeric matrix. The first
numeric matrix. The first 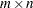 submatrix contains the constant terms of the polynomials, the second
submatrix contains the constant terms of the polynomials, the second 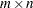 submatrix contains the first-order terms, and so on.
submatrix contains the first-order terms, and so on. - b
is an
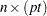 matrix. The first
matrix. The first 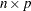 submatrix contains the constant terms of the polynomials, the second
submatrix contains the constant terms of the polynomials, the second 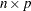 submatrix contains the first-order terms, and so on.
submatrix contains the first-order terms, and so on. - dim
is a
 matrix, with value
matrix, with value 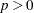 . The value of this matrix is used to set the dimension
. The value of this matrix is used to set the dimension 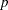 of the matrix
of the matrix 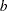 . If omitted, the value of
. If omitted, the value of 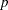 is set to 1.
is set to 1.
The PRODUCT function multiplies matrices of polynomials. The value returned is the 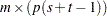 matrix of the polynomial products. The first
matrix of the polynomial products. The first 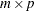 submatrix contains the constant terms, the second
submatrix contains the constant terms, the second 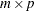 submatrix contains the first-order terms, and so on.
submatrix contains the first-order terms, and so on.
The PRODUCT function can be used to multiply the matrix operators employed in a multivariate time series model of the form
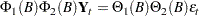 |
where 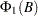 ,
, 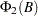 ,
, 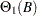 , and
, and 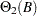 are matrix polynomial operators whose first matrix coefficients are identity matrices. Often
are matrix polynomial operators whose first matrix coefficients are identity matrices. Often 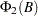 and
and 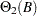 represent seasonal components that are isolated in the modeling process but multiplied with the other operators when forming predictors or estimating parameters. The RATIO function is often employed in a time series context as well.
represent seasonal components that are isolated in the modeling process but multiplied with the other operators when forming predictors or estimating parameters. The RATIO function is often employed in a time series context as well.
For example, the following statements demonstrate the PRODUCT function:
m1 = {1 2 3 4,
5 6 7 8};
m2 = {1 2 3,
4 5 6};
r = product(m1, m2, 1);
print r;
| r | |||
|---|---|---|---|
| 9 | 31 | 41 | 33 |
| 29 | 79 | 105 | 69 |