| MAD Function |
The MAD function computes the univariate (scaled) median absolute deviation of each column of the input matrix.
The arguments to the MAD function are as follows:
- x
is an
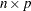 input data matrix.
input data matrix. - method
-
is an optional string argument with the following values:
- "MAD"
for computing the median absolute deviation (MAD); this is the default.
- "NMAD"
for computing the normalized version of MAD
- "SN"
for computing
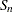
- "QN"
for computing
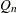
For simplicity, the following descriptions assume that the input argument x is a column vector. The notation 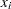 means the
means the 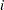 th element of the column vector x.
th element of the column vector x.
The MAD function can be used for computing one of the following three robust scale estimates:
-
median absolute deviation (MAD) or normalized form of MAD,
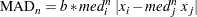
where
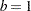 is the unscaled default and
is the unscaled default and 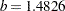 is used for the scaled version (consistency with the Gaussian distribution).
is used for the scaled version (consistency with the Gaussian distribution). -
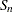 , which is a more efficient alternative to MAD,
, which is a more efficient alternative to MAD, 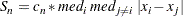
where the outer median is a low median (order statistic of rank
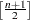 ) and the inner median is a high median (order statistic of rank
) and the inner median is a high median (order statistic of rank 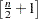 ), and where
), and where 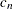 is a scalar that depends on sample size
is a scalar that depends on sample size  .
. -
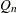 is another efficient alternative to MAD. It is based on the
is another efficient alternative to MAD. It is based on the 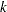 th-order statistic of the
th-order statistic of the 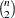 inter-point distances,
inter-point distances, 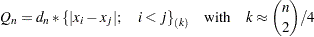
where
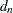 is a scalar similar to but different from
is a scalar similar to but different from 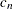 . See Rousseeuw and Croux (1993) for more details.
. See Rousseeuw and Croux (1993) for more details.
The scalars 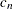 and
and 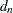 are defined as follows:
are defined as follows:
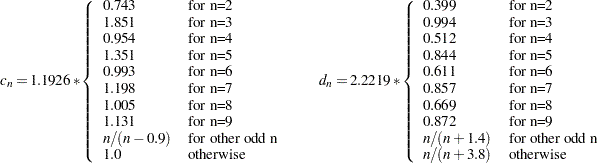 |
Example
The following example uses the univariate data set of Barnett and Lewis (1978). The data set is used in Chapter 12 to illustrate the univariate LMS and LTS estimates.
b = {3, 4, 7, 8, 10, 949, 951};
rmad1 = mad(b);
rmad2 = mad(b,"mad");
rmad3 = mad(b,"nmad");
rmad4 = mad(b,"sn");
rmad5 = mad(b,"qn");
print "Default MAD=" rmad1,
"Common MAD =" rmad2,
"MAD*1.4826 =" rmad3,
"Robust S_n =" rmad4,
"Robust Q_n =" rmad5;
| rmad1 | |
|---|---|
| Default MAD= | 4 |
| rmad2 | |
|---|---|
| Common MAD = | 4 |
| rmad3 | |
|---|---|
| MAD*1.4826 = | 5.9304089 |
| rmad4 | |
|---|---|
| Robust S_n = | 7.143674 |
| rmad5 | |
|---|---|
| Robust Q_n = | 5.7125049 |