| LCP Call |
The LCP subroutine solves the linear complementarity problem:
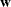 |
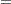 |
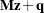 |
|||
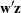 |
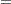 |
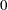 |
|||
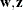 |
 |
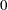 |
That is, given a matrix 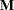 and a vector
and a vector 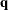 , the LCP subroutine computes orthogonal, nonnegative vectors
, the LCP subroutine computes orthogonal, nonnegative vectors 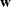 and
and  which satisfy the previous equations.
which satisfy the previous equations.
The input arguments to the LCP subroutine are as follows:
- m
is an
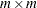 matrix.
matrix. - q
is an
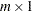 matrix.
matrix. - epsilon
-
is a scalar that defines virtual zero. The default value of epsilon is 1E
 8.
8. The LCP subroutine returns the following matrices:
- rc
-
returns one of the following scalar return codes:
rc
Termination
0
A solution is found.
1
No solution is possible.
5
The solution is numerically unstable.
6
The subroutine could not obtain enough memory.
- w
returns an
 -element column vector
-element column vector - z
returns an
 -element column vector
-element column vector
The following statements give a simple example:
q = {1, 1};
m = {1 0,
0 1};
call lcp(rc, w, z, m, q);
print rc, w, z;
| rc |
|---|
| 0 |
| w |
|---|
| 1 |
| 1 |
| z |
|---|
| 0 |
| 0 |
The next example shows the relationship between quadratic programming and the linear complementarity problem. Consider the linearly constrained quadratic program:
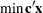 |
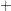 |
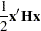 |
|||
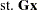 |
 |
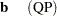 |
|||
 |
 |
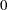 |
If 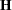 is positive semidefinite, then a solution to the Kuhn-Tucker conditions solves QP. The Kuhn-Tucker conditions for QP are
is positive semidefinite, then a solution to the Kuhn-Tucker conditions solves QP. The Kuhn-Tucker conditions for QP are
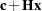 |
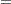 |
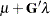 |
|||
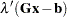 |
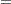 |
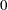 |
|||
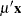 |
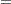 |
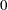 |
|||
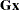 |
 |
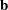 |
|||
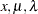 |
 |
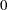 |
In the linear complementarity problem, let
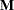 |
 |
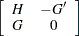 |
|||
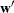 |
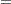 |
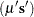 |
|||
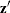 |
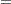 |
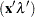 |
|||
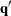 |
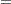 |
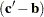 |
Then the Kuhn-Tucker conditions are expressed as finding 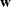 and
and  that satisfy
that satisfy
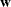 |
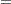 |
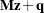 |
|||
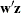 |
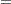 |
 |
|||
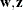 |
 |
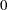 |
From the solution 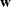 and
and  to this linear complementarity problem, the solution to QP is obtained; namely,
to this linear complementarity problem, the solution to QP is obtained; namely,  is the primal structural variable,
is the primal structural variable, 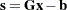 the surpluses, and
the surpluses, and 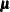 and
and 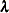 are the dual variables. Consider a quadratic program with the following data:
are the dual variables. Consider a quadratic program with the following data:
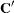 |
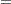 |
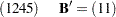 |
|||
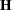 |
 |
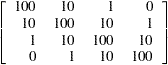 |
|||
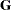 |
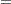 |
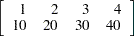 |
This problem is solved by using the LCP subroutine as follows:
/*---- Data for the Quadratic Program -----*/
c = {1, 2, 3, 4};
h = {100 10 1 0, 10 100 10 1, 1 10 100 10, 0 1 10 100};
g = {1 2 3 4, 10 20 30 40};
b = {1, 1};
/*----- Express the Kuhn-Tucker Conditions as an LCP ----*/
m = h || -g`;
m = m // (g || j(nrow(g),nrow(g),0));
q = c // -b;
/*----- Solve for a Kuhn-Tucker Point --------*/
call lcp(rc, w, z, m, q);
/*------ Extract the Solution to the Quadratic Program ----*/
x = z[1:nrow(h)];
print rc x;
| rc | x |
|---|---|
| 0 | 0.0307522 |
| 0.0619692 | |
| 0.0929721 | |
| 0.1415983 |