| INVUPDT Function |
The INVUPDT function updates a matrix inverse.
The arguments to the INVUPDT function are as follows:
- matrix
is an
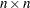 nonsingular matrix. In most applications matrix is symmetric positive definite.
nonsingular matrix. In most applications matrix is symmetric positive definite. - vector
is an
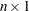 or
or 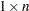 vector.
vector. - scalar
is a numeric scalar.
The Sherman-Morrison-Woodbury formula is
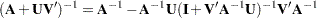 |
where 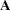 is an
is an 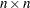 nonsingular matrix and
nonsingular matrix and 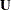 and
and 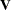 are
are 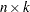 . The formula shows that a rank
. The formula shows that a rank 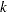 update to
update to 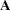 corresponds to a rank
corresponds to a rank 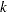 update of
update of 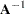 .
.
The INVUPDT function implements the Sherman-Morrison-Woodbury formula for rank-one updates with 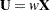 and
and 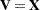 , where
, where 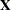 is an
is an 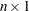 vector and
vector and 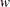 is a scalar.
is a scalar.
If 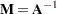 , then you can call the INVUPDT function as follows:
, then you can call the INVUPDT function as follows:
R = invupdt(M, X, w);
This statement computes the following matrix:
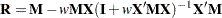 |
The matrix 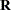 is equivalent to
is equivalent to 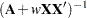 . If
. If 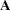 is symmetric positive definite, then so is
is symmetric positive definite, then so is 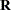 .
.
If 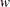 is not specified, then it is given a default value of
is not specified, then it is given a default value of  .
.
A common use of the INVUPDT function is in linear regression. If 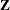 is a design matrix,
is a design matrix, 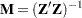 is the associated inverse crossproduct matrix, and
is the associated inverse crossproduct matrix, and  is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that includes the new observation can be updated from
is a new observation to be used in estimating the parameters of a linear model, then the inverse crossproducts matrix that includes the new observation can be updated from 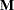 by using the following statement:
by using the following statement:
M2 = invupdt(M, v);
If 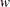 is
is  , the function adds an observation to the inverse; if
, the function adds an observation to the inverse; if 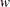 is
is 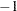 , the function removes an observation from the inverse. If weighting is used,
, the function removes an observation from the inverse. If weighting is used, 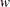 is the weight.
is the weight.
To perform the computation, the INVUPDT function uses about 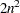 multiplications and additions, where
multiplications and additions, where  is the row dimension of the positive definite argument matrix.
is the row dimension of the positive definite argument matrix.
The following program demonstrates adding or removing observations from a linear fit and updating the inverse crossproduct matrix:
X = {0, 1, 1, 1, 2, 2, 3, 4, 4};
Y = {1, 1, 2, 6, 2, 3, 3, 3, 4};
/* find linear fit */
Z = j(nrow(X), 1, 1) || X; /* design matrix */
M = inv(Z`*Z);
b = M*Z`*Y; /* LS estimate */
resid = Y - Z*b; /* residuals */
print "Original Fit", b resid;
/* residual for observation (1,6) seems too large.
Take obs number 4 out of data set and refit. */
v = z[4,];
M = invupdt(M, v, -1); /* update inverse crossprod */
keepObs = (1:3) || (5:nrow(X));
Z = Z[keepObs, ];
Y = Y[keepObs, ];
b = M*Z`*Y; /* new LS estimate */
print "After deleting observation 4", b;
/* Add a new obs (x,y) = (0,2) and refit. */
obs = {0 2};
v = 1 || obs[1]; /* new row in design matrix */
M = invupdt(M, v);
Z = Z // v;
Y = Y // obs[2];
b = M*Z`*Y; /* new LS estimate */
print "After adding observation (0,2)", b;
| Original Fit |
| b | resid |
|---|---|
| 2.0277778 | -1.027778 |
| 0.375 | -1.402778 |
| -0.402778 | |
| 3.5972222 | |
| -0.777778 | |
| 0.2222222 | |
| -0.152778 | |
| -0.527778 | |
| 0.4722222 |
| After deleting observation 4 |
| b |
|---|
| 1 |
| 0.6470588 |
| After adding observation (0,2) |
| b |
|---|
| 1.3 |
| 0.5470588 |