Language Reference: HOMOGEN Function

HOMOGEN Function

HOMOGEN( matrix ) ;

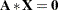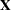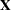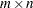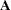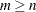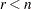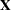The HOMOGEN function solves the homogeneous system of linear equations $\text{[math]}$ for $\text{[math]}$ . For at least one solution vector $\text{[math]}$ to exist, the $\text{[math]}$ matrix $\text{[math]}$ , $\text{[math]}$ , has to be of rank $\text{[math]}$ . The HOMOGEN function computes an $\text{[math]}$ column orthonormal matrix $\text{[math]}$ with the properties that 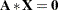$\text{[math]}$ and $\text{[math]}$ . 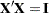In other words, the columns of 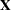$\text{[math]}$ form an orthonormal basis for the nullspace of $\text{[math]}$ .

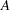If 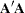$\text{[math]}$ is ill-conditioned, rounding-error problems can occur in determining the correct rank of 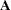$\text{[math]}$ and in determining the correct number of solutions $\text{[math]}$ .

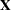The following statements compute an example from Wilkinson and Reinsch (1971):

a = {22  10   2   3   7,
     14   7  10   0   8,
     -1  13  -1 -11   3,
     -3  -2  13  -2   4,
      9   8   1  -2   4,
      9   1  -7   5  -1,
      2  -6   6   5   1,
      4   5   0  -2   2};
x = homogen(a);
print x;

Figure 23.134 Solutions to a Homogeneous System

x
-0.419095	0
0.4405091	0.4185481
-0.052005	0.3487901
0.6760591	0.244153
0.4129773	-0.802217

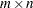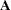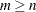In addition, you can use the HOMOGEN function to determine the rank of an $\text{[math]}$ matrix $\text{[math]}$ where $\text{[math]}$ by counting the number of columns in the matrix $\text{[math]}$ .

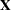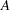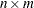If $\text{[math]}$ is an $\text{[math]}$ matrix, then, in addition to the memory allocated for the return matrix, the HOMOGEN function temporarily allocates an 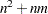$\text{[math]}$ array for performing its computation.