| DET Function |
DET(
square-matrix )
;
The DET function computes the determinant of a square matrix. The determinant, the product of the eigenvalues, is a scalar numeric value. If the determinant of a matrix is zero, then the matrix is singular. A singular matrix does not have an inverse.
The DET function performs an LU decomposition and collects the product of the diagonals (Forsythe, Malcom, and Moler; 1967). For a matrix with  rows, the DET function allocates a temporary
rows, the DET function allocates a temporary 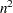 array in order to compute the determinant.
array in order to compute the determinant.
The following statements compute the determinant of a matrix:
a = {1 1 1,
1 2 4,
1 3 9};
d = det(a);
print d;
Figure 23.87
Determinant of a Matrix
| d |
|---|
| 2 |
The DET function uses a criterion to determine whether the input matrix is singular. See the INV function for details.