| ALLPERM Function |
The ALLPERM function generates all permutations of a set with  elements. The permutations are produced in the same order and using the same algorithm (Trotter; 1962) as the ALLPERM function in Base SAS software.
elements. The permutations are produced in the same order and using the same algorithm (Trotter; 1962) as the ALLPERM function in Base SAS software.
By default, the ALLPERM function returns a matrix with 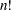 rows and
rows and  columns. Each row of the returned matrix represents a single permutation. The following statements generate all permutations of the set
columns. Each row of the returned matrix represents a single permutation. The following statements generate all permutations of the set 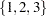 :
:
n = 3; p = allperm(n); print p;
| p | ||
|---|---|---|
| 1 | 2 | 3 |
| 1 | 3 | 2 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 1 | 3 |
The first argument can be a scalar or a vector. If it is a vector, the number of elements in the vector determines the value of  . The ALLPERM function can compute permutations of arbitrary numeric or character matrices. For example, the following statements compute permutations of an unsorted character vector:
. The ALLPERM function can compute permutations of arbitrary numeric or character matrices. For example, the following statements compute permutations of an unsorted character vector:
a = allperm({C B A});
print a;
| a | ||
|---|---|---|
| C | B | A |
| C | A | B |
| A | C | B |
| A | B | C |
| B | A | C |
| B | C | A |
The optional second argument, idx, can be used to control the number of rows in the output of the function. The argument must consist of consecutive integers; you cannot use it to randomly access permutations that are out of sequence. The second argument is often used to generate one or more permutations in a loop so that you do not need to allocate a huge matrix that contains all of the permutations at once. The following statements illustrate this usage:
perm = 1:n; do i=1 to fact(n); perm = allperm(perm, i); /* do something with the i_th permutation */ end;
If you want the permutations in lexicographic order, generate the permutations and then use the SORT subroutine, as follows:
p = allperm(n); call sort(p, 1:n);