Example 20.4 Optimization with Linear Constraints Using Repair Strategy
This problem seeks a minimum within a convex domain specified by a convex hull, a set of points such that all points in the search space are normalized linear combinations of those points. Each solution is represented by a set of weights 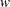 such that there is one
such that there is one 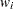 for each point in the convex hull,
for each point in the convex hull, 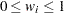 , and
, and 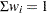 . In this example the feasible region is the convex hull defined by the set of points (-3 -2), (3 -2), (-3 2), and (3 2). The objective function is a six-hump camel-back function (see Michalewicz (1996), Appendix B), with a known global minimum value of -1.0316 at two different points, (-0.0898,0.7126) and (0.0898,-0.7126). A user mutation module is specified, and the simple crossover operator is used. Both the mutation operator and the crossover operator will produce solutions that violate the constraints, so in the objective function each solution will be checked and renormalized to bring it back within the convex hull.
. In this example the feasible region is the convex hull defined by the set of points (-3 -2), (3 -2), (-3 2), and (3 2). The objective function is a six-hump camel-back function (see Michalewicz (1996), Appendix B), with a known global minimum value of -1.0316 at two different points, (-0.0898,0.7126) and (0.0898,-0.7126). A user mutation module is specified, and the simple crossover operator is used. Both the mutation operator and the crossover operator will produce solutions that violate the constraints, so in the objective function each solution will be checked and renormalized to bring it back within the convex hull.
proc iml;
/* Test case using user modules for the mutation operator and
* for initialization
*/
start sixhump(w) global(cvxhull);
/* Function has global minimum value of -1.0316
* at x = {-0.0898 0.7126} and
* x = { 0.0898 -0.7126}
*/
sum = w[1,+];
/* guard against the remote possibility of all-0 weights */
if sum=0 then do;
nc = ncol(w);
w = j(1, nc, 1/nc );
sum = 1;
end;
/* re-normalize weights */
w = w/sum;
/* convert to x-coordinate form */
x = (w * cvxhull)[+,];
x1 = x[1];
x2 = x[2];
/* compute objective value */
r = (4 - 2.1*x1##2 + x1##4/3)*x1##2 + x1*x2 +
(-4 + 4*x2*x2)*x2##2;
return(r);
finish;
/* each row is one point on the boundary of
* the convex hull */
cvxhull = {-3 -2,
3 -2,
-3 2,
3 2};
/* initialization module */
start cvxinit( w ) global(cvxhull);
sum = 0;
a = j(1, nrow(cvxhull), 1234);
do while(sum = 0);
r = uniform(a);
sum = r[1,+];
end;
w = r / sum;
finish;
/* mutation module */
start cvxmut(w)global(cvxhull);
row = int(uniform(1234) * nrow(cvxhull)) + 1;
r = uniform(1234);
w[1,row] = r;
finish;
id = gasetup(1, /* real fixed-length vector encoding */
nrow(cvxhull), /* vector size = number of points
* specifying convex hull
*/
1234);
call gasetobj(id,
0, /* minimize a user-specified objective function */
"sixhump"
);
call gasetsel( id,
5, /* carry over the best 5 from each generation */
1, /* dual tournament */
0.95 /* best-player-wins probability */
);
call gasetcro(id,
0.8, /* crossover probability */
1 /* simple crossover operator */
);
call gasetmut(id,0.05,0,"cvxmut");
call gainit( id,
100, /* population size */
, /* not using constant bounds */
"cvxinit" /* initialization module */
);
niter = 35; /* number of iterations */
summary = j(niter,2);
mattrib summary [c = {"bestValue", "avgValue"}];
call gagetval(value, id);
summary[1,1] = value[1];
summary[1,2] = value[:];
do i = 1 to niter;
call garegen(id);
call gagetval(value, id);
summary[i,1] = value[1];
summary[i,2] = value[:];
end;
call gagetmem(mem, value, id, 1);
bestX = (mem * cvxhull)[+,];
print "best X " bestX[l = ""],
"best value " value[l = ""];
iteration = t(1:niter);
print iteration summary;
call gaend(id);
The output results are
best X 0.089842 -0.712658
best value -1.031628
SUMMARY
ITERATION bestValue avgValue
1 -0.082301 0.9235856
2 -0.948434 0.1262678
3 -0.956136 0.2745601
4 -1.017636 0.1367912
5 -1.028457 -0.241069
6 -1.028457 -0.353218
7 -1.028457 -0.56789
8 -1.028457 -0.73044
9 -1.028457 -0.854496
10 -1.028509 -0.941693
11 -1.031334 -0.936541
12 -1.031334 -0.90363
13 -1.031373 -0.774917
14 -1.031614 -0.873418
15 -1.031614 -0.886818
16 -1.031618 -0.95678
17 -1.031619 -0.933061
18 -1.031626 -0.885132
19 -1.031628 -0.936944
20 -1.031628 -0.906637
21 -1.031628 -0.925809
22 -1.031628 -0.860156
23 -1.031628 -0.946146
24 -1.031628 -0.817196
25 -1.031628 -0.883284
26 -1.031628 -0.904361
27 -1.031628 -0.974893
28 -1.031628 -0.975647
29 -1.031628 -0.872004
30 -1.031628 -1.031628
31 -1.031628 -0.897558
32 -1.031628 -0.922121
33 -1.031628 -0.855045
34 -1.031628 -0.922061
35 -1.031628 -0.958257
Any problem with linear constraints could be formulated in this way, by determining the convex hull that corresponds to the constraints. The genetic operators and the repair strategy are straightforward to apply, and as this case shows, can give reasonable convergence to a global optimum.