| Choosing the Problem Encoding |
Problem encoding refers to the structure or type of solution space that is to be optimized, such as real-valued fixed-length vectors or integer sequences. IML offers encoding options appropriate to several types of optimization problems.
General Numeric Matrix: With this encoding, solutions can take the form of a numeric matrix of any shape. Also, different solutions can have different dimensions. This is the most flexible option. If you use this encoding, IML makes no assumptions about the form of the solution, so you are required to specify user modules for crossover and mutation operators, and a user module for creating the initial solution population.
Fixed-Length Real-Valued Row Vector: If you use this encoding, you must also specify the number of components in the solution vector. Using this option, you can use some IML-supplied crossover and mutation operators later, or you can supply custom modules. You can also specify upper and lower bounds for each component in the vector, and IML will generate an initial population for the GA randomly distributed between the bounds. If you don’t explicitly set crossover and mutation operators, IML will provide default operators to be used in the optimization. This type of encoding is often used for general nonlinear optimization problems.
Fixed-Length Integer-Valued Row Vector: This option is similar to the fixed-length real-valued encoding already described, except that the IML-supplied genetic operators and initialization process will preserve and generate integer solutions. This type of encoding might be applicable, for example, in an assignment problem where the positions within the vector represent different tasks, and the integer values represent different machines or other resources that might be applied to each task.
Fixed-Length Integer Sequence: In this encoding, each solution is composed of a sequence of integers ranging from 1 to the length of the sequence, with different solutions distinguished by different ordering of the elements. For example, 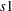 and
and  are two integer sequences of length 6:
are two integer sequences of length 6:
s1 = {1 2 3 4 5 6};
s2 = {2 6 5 3 4 1};
This type of encoding is often used for routing problems like the traveling salesman problem, where each element represents a city in a circular route, or scheduling problems.