Working with Matrices: Functions That Generate Matrices

Working with Matrices

Functions That Generate Matrices

SAS/IML software has many useful built-in functions that generate matrices. For example, the J function creates a matrix with a given dimension and specified element value. You can use this function to initialize a matrix to a predetermined size. Here are several functions that generate matrices:

BLOCK: creates a block-diagonal matrix
DESIGNF: creates a full-rank design matrix
I: creates an identity matrix
J: creates a matrix of a given dimension
REPEAT: creates a new matrix by repeating elements of the argument matrix
SHAPE: shapes a new matrix from the argument

The sections that follow illustrate the functions that generate matrices. The output of each example is generated automatically by using the RESET PRINT statement:

reset print;

The BLOCK Function

The BLOCK function has the following general form:

BLOCK (matrix1,<matrix2,...,matrix15>) ;

The BLOCK function creates a block-diagonal matrix from the argument matrices. For example, the following statements form a block-diagonal matrix:

a = {1 1, 1 1};
b = {2 2, 2 2};
c = block(a,b);

Figure 5.8 A Block-Diagonal Matrix

c 4 rows 4 cols (numeric)

1	1	0	0
1	1	0	0
0	0	2	2
0	0	2	2

The J Function

The J function has the following general form:

J (nrow <,ncol <,value>>) ;

It creates a matrix that has nrow rows, ncol columns, and all elements equal to value. The ncol and value arguments are optional; if they are not specified, default values are used. In many statistical applications, it is helpful to be able to create a row (or column) vector of ones. (You did so to calculate coffee totals in the previous section.) You can do this with the J function. For example, the following statement creates a 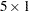$\text{[math]}$ column vector of ones:

ones = j(5,1,1);

Figure 5.9 A Vector of Ones

ones 5 rows 1 col (numeric)

The I Function

The I function creates an identity matrix of a given size. It has the following general form:

I (dimension) ;

where dimension gives the number of rows. For example, the following statement creates a 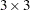$\text{[math]}$ identity matrix:

I3 = I(3);

Figure 5.10 An Identity Matrix

I3 3 rows 3 cols (numeric)

1	0	0
0	1	0
0	0	1

The DESIGNF Function

The DESIGNF function generates a full-rank design matrix, which is useful in calculating ANOVA tables. It has the following general form:

DESIGNF (column-vector) ;

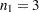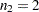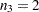For example, the following statement creates a full-rank design matrix for a one-way ANOVA, where the treatment factor has three levels and there are $\text{[math]}$ , $\text{[math]}$ , and $\text{[math]}$ observations at the factor levels:

d = designf({1,1,1,2,2,3,3});

Figure 5.11 A Design Matrix

d 7 rows 2 cols (numeric)

1	0
1	0
1	0
0	1
0	1
-1	-1
-1	-1

The REPEAT Function

The REPEAT function creates a new matrix by repeating elements of the argument matrix. It has the following syntax:

REPEAT (matrix, nrow, ncol) ;

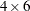The function repeats matrix a total of nrow $\text{[math]}$ ncol times. The argument is repeated nrow times in the vertical direction and ncol times in the horizontal direction. For example, the following statement creates a $\text{[math]}$ matrix:

x = {1 2, 3 4};
r = repeat(x, 2, 3);

Figure 5.12 A Matrix of Repeated Values

x 2 rows 2 cols (numeric)

1	2	1	2	1	2
3	4	3	4	3	4
1	2	1	2	1	2
3	4	3	4	3	4

The SHAPE Function

The SHAPE function creates a new matrix by reshaping an argument matrix. It has the following general form:

SHAPE (matrix, nrow <,ncol <,pad-value>>) ;

The ncol and pad-value arguments are optional; if they are not specified, default values are used. The following statement uses the SHAPE function to create a 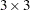$\text{[math]}$ matrix that contains the values 99 and 33. The function cycles back and repeats values to fill in the matrix when no pad-value is given.

aa = shape({99 33, 33 99}, 3, 3);

Figure 5.13 A Matrix of Repeated Values

r 4 rows 6 cols (numeric)

99	33	33
99	99	33
33	99	99

Alternatively, you can specify a value for pad-value that is used for filling in the matrix:

bb = shape({99 33, 33 99}, 3, 3, 0);

Figure 5.14 A Matrix Padded with Zeroes

aa 3 rows 3 cols (numeric)

99	33	33
99	0	0
0	0	0

The SHAPE function cycles through the argument matrix elements in row-major order and fills in the matrix with zeros after the first cycle through the argument matrix.

Top of Page