| Nonlinear Optimization Examples |
| Kuhn-Tucker Conditions |
The nonlinear programming (NLP) problem with one objective function 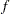 and
and  constraint functions
constraint functions 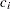 , which are continuously differentiable, is defined as follows:
, which are continuously differentiable, is defined as follows:
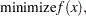 |
 |
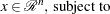 |
|||
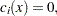 |
 |
 |
|||
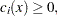 |
 |
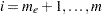 |
In the preceding notation,  is the dimension of the function
is the dimension of the function 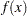 , and
, and 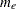 is the number of equality constraints. The linear combination of objective and constraint functions
is the number of equality constraints. The linear combination of objective and constraint functions
 |
is the Lagrange function, and the coefficients 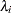 are the Lagrange multipliers.
are the Lagrange multipliers.
If the functions 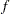 and
and 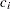 are twice differentiable, the point
are twice differentiable, the point  is an isolated local minimizer of the NLP problem, if there exists a vector
is an isolated local minimizer of the NLP problem, if there exists a vector 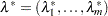 that meets the following conditions:
that meets the following conditions:
Kuhn-Tucker conditions
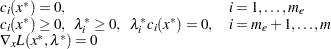
second-order condition
Each nonzero vector
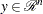 with
with 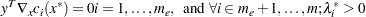
satisfies
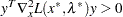
In practice, you cannot expect the constraint functions 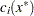 to vanish within machine precision, and determining the set of active constraints at the solution
to vanish within machine precision, and determining the set of active constraints at the solution  might not be simple.
might not be simple.
Copyright © SAS Institute, Inc. All Rights Reserved.