| Module Library |
| RANDMVT Function |
generates a random sample from a multivariate Student’s  distribution
distribution
- RANDMVT( N, DF, Mean, Cov ) ;
The inputs are as follows:
- N
is the number of desired observations sampled from the multivariate Student’s
 distribution.
distribution. - DF
is a scalar value that represents the degrees of freedom for the
 distribution.
distribution. - Mean
is a
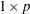 vector of means.
vector of means. - Cov
is a
 symmetric positive definite variance-covariance matrix.
symmetric positive definite variance-covariance matrix.
The RANDMVT function returns an 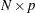 matrix that contains
matrix that contains 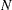 random draws from the Student’s
random draws from the Student’s  distribution with DF degrees of freedom, mean vector Mean, and covariance matrix Cov.
distribution with DF degrees of freedom, mean vector Mean, and covariance matrix Cov.
If 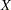 follows a multivariate
follows a multivariate  distribution with
distribution with  degrees of freedom, mean vector
degrees of freedom, mean vector 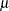 , and variance-covariance matrix
, and variance-covariance matrix 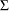 , then
, then
the probability density function for
 is
is 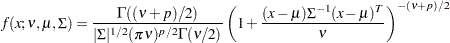
if
 , the probability density function reduces to a univariate Student’s
, the probability density function reduces to a univariate Student’s  distribution.
distribution. the expected value of
 is
is  .
. the covariance of
 and
and 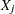 is
is  when
when 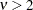 .
.
The following example generates 1000 samples from a two-dimensional  distribution with 7 degrees of freedom, mean vector
distribution with 7 degrees of freedom, mean vector 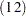 , and covariance matrix S. Each row of the returned matrix x is a row vector sampled from the
, and covariance matrix S. Each row of the returned matrix x is a row vector sampled from the  distribution. The example then computes the sample mean and covariance and compares them with the expected values. Here are the code and the output:
distribution. The example then computes the sample mean and covariance and compares them with the expected values. Here are the code and the output:
call randseed(1);
N=1000;
DF = 4;
Mean = {1 2};
S = {1 1, 1 5};
x = RandMVT( N, DF, Mean, S );
SampleMean = x[:,];
n = nrow(x);
y = x - repeat( SampleMean, n );
SampleCov = y`*y / (n-1);
Cov = (DF/(DF-2)) * S;
print SampleMean Mean, SampleCov Cov;
SampleMean Mean
1.0768636 2.0893911 1 2
SampleCov Cov
1.8067811 1.8413406 2 2
1.8413406 9.7900638 2 10
In the preceding example, the columns (marginals) of x do not follow univariate  distributions. If you want a sample whose marginals are univariate
distributions. If you want a sample whose marginals are univariate  , then you need to scale each column of the output matrix:
, then you need to scale each column of the output matrix:
x = RandMVT( N, DF, Mean, S ); StdX = x / sqrt(diag(S)); /* StdX columns are univariate t */
Equivalently, you can generate samples whose marginals are univariate  by passing in a correlation matrix instead of a general covariance matrix.
by passing in a correlation matrix instead of a general covariance matrix.
For further details about sampling from the multivariate  distribution, see Kotz and Nadarajah (2004).
distribution, see Kotz and Nadarajah (2004).
Copyright © SAS Institute, Inc. All Rights Reserved.