The VTSROOT subroutine computes the characteristic roots of the model from AR and MA characteristic functions.

The input arguments to the VTSROOT subroutine are as follows:

phi

specifies a 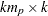matrix that contains the autoregressive coefficient matrices, where 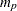is the number of the elements in the subset of the AR order and 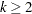is the number of variables. You must specify either phi or theta.

theta

specifies a matrix that contains the moving average coefficient matrices, where 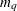is the number of the elements in the subset of the MA order. You must specify either phi or theta.

p

specifies the subset of the AR order. See the VARMACOV subroutine.

q

specifies the subset of the MA order. See the VARMACOV subroutine.

The VTSROOT subroutine returns the following value:

root

is a matrix, where is the maximum order of the AR characteristic function and is the maximum order of the MA characteristic function. The first rows refer to the results of the AR characteristic function; the last rows refer to the results of the MA characteristic function.

The first column contains the real parts, , of eigenvalues of companion matrix associated with the AR() or MA() characteristic function; the second column contains the imaginary parts, 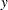, of the eigenvalues; the third column contains the moduli of the eigenvalues, ; the fourth column contains the arguments () of the eigenvalues, measured in radians from the positive real axis. The fifth column contains the arguments expressed in degrees rather than radians.

Consider the roots of the characteristic functions, and , where is an identity matrix with dimension 2 and

To compute these roots, you can use the following statements:

  phi  = { 1.2 -0.5, 0.6 0.3 };
  theta= {-0.6  0.3, 0.3 0.6 };
  call vtsroot(root, phi, theta);