| Language Reference |
| SWEEP Function |
The SWEEP function sweeps matrix on the pivots indicated in index-vector to produce a new matrix.
The arguments the SWEEP function are as follows:
- matrix
is a numeric matrix or literal.
- index-vector
is a numeric vector that indicates the pivots.
The values of the index vector must be less than or equal to the number of rows or the number of columns in matrix, whichever is smaller.
For example, suppose that 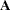 is partitioned into
is partitioned into
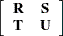 |
such that  is
is 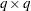 and
and 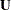 is
is 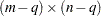 . Let
. Let
I = [1 2 3 . . . q]
Then, the statement
B=sweep(A,I);
becomes
 |
The index vector can be omitted. In this case, the function sweeps the matrix on all pivots on the main diagonal 1:MIN(nrow,ncol).
The SWEEP function has sequential and reversibility properties when the submatrix swept is positive definite:
SWEEP(SWEEP(
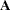 ,1),2)=SWEEP(
,1),2)=SWEEP(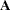 ,{ 1 2 })
,{ 1 2 }) SWEEP(SWEEP(
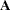 ,
,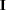 ),
),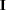 )=
)=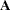
See Beaton (1964) for more information about these properties.
To use the SWEEP function for regression, suppose the matrix 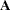 contains
contains
 |
where  is
is  .
.
Then  contains
contains
 |
The partitions of 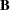 form the beta values, SSE, and a matrix proportional to the covariance of the beta values for the least squares estimates of
form the beta values, SSE, and a matrix proportional to the covariance of the beta values for the least squares estimates of 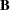 in the linear model
in the linear model
 |
If any pivot becomes very close to zero (less than or equal to 1E 12), the row and column for that pivot are zeroed. See Goodnight (1979) for more information.
12), the row and column for that pivot are zeroed. See Goodnight (1979) for more information.
An example that uses the SWEEP function for regression follows:
x = { 1 1 1,
1 2 4,
1 3 9,
1 4 16,
1 5 25,
1 6 36,
1 7 49,
1 8 64 };
y = { 3.929,
5.308,
7.239,
9.638,
12.866,
17.069,
23.191,
31.443 };
n = nrow(x); /* number of observations */
k = ncol(x); /* number of variables */
xy = x||y; /* augment design matrix */
A = xy` * xy; /* form cross products */
S = sweep( A, 1:k );
beta = S[1:k,4]; /* parameter estimates */
sse = S[4,4]; /* sum of squared errors */
mse = sse / (n-k); /* mean squared error */
cov = S[1:k, 1:k] # mse; /* covariance of estimates */
print cov, beta, sse;
COV
0.9323716 -0.436247 0.0427693
-0.436247 0.2423596 -0.025662
0.0427693 -0.025662 0.0028513
BETA
5.0693393
-1.109935
0.5396369
SSE
2.395083
The SWEEP function performs most of its computations in the memory allocated for the result matrix.
Copyright © SAS Institute, Inc. All Rights Reserved.