If 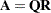is the QR decomposition of the matrix , the RUPDT subroutine enables you to efficiently recompute the matrix when a new row is added to 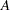. This is called an update. Similarly, the RDODT subroutine enables you to efficiently recompute the matrix when an existing row is deleted from 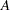. This is called a downdate. You can also use the RDODT and RUPDT subroutines to downdate and update Cholesky decompositions.

The RDODT and RUPDT subroutines return the values:

def

is only used for downdating, and it specifies whether the downdating of matrix 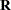by using the 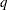rows in argument has been successful. The result def=2 means that the downdating of 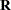by at least one row of 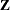leads to a singular matrix and cannot be completed successfully (since the result of downdating is not unique). In that case, the results rup, bup, and sup contain missing values only. The result def=1 means that the residual sum of squares, ssq, could not be downdated successfully and the result sup contains missing values only. The result def=0 means that the downdating of 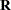by 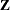was completed successfully.

rup

is the upper triangular matrix 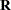that has been updated or downdated by using the 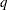rows in .

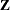bup

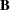is the matrix of right-hand sides that has been updated or downdated by using the 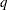rows in argument 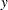. If the argument is not specified, bup is not computed.

sup

is a 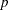vector of square roots of residual sum of squares that is updated or downdated by using the 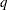rows of argument 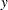. If ssq is not specified, sup is not computed.

The input arguments to the RDODT and RUPDT subroutines are as follows:

r

specifies an upper triangular matrix 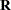to be updated or downdated by the 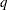rows in 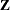. Only the upper triangle of 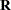is used; the lower triangle can contain any information.

z

specifies a 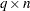matrix 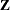used rowwise to update or downdate the matrix .

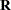b

specifies an optional matrix 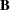of right-hand sides that have to be updated or downdated simultaneously with 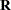. If is specified, the argument 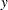must also be specified.

y

specifies an optional matrix 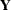used rowwise to update or downdate the right-hand side matrix 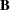. If is specified, the argument 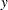must also be specified.

ssq

is an optional 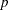vector that, if is specified, specifies the square root of the error sum of squares that should be updated or downdated simultaneously with 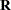and .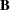

The upper triangular matrix 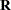of the QR decomposition of an 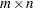matrix ,

is recomputed efficiently in two cases:

• update: An vector is added to matrix .

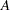• downdate: An vector is deleted from matrix .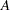

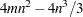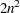Computing the whole QR decomposition of matrix by Householder transformations requires floating-point operations, whereas updating or downdating the QR decomposition (by Givens rotations) of one row vector requires only floating-point operations.

If the QR decomposition is used to solve the full-rank linear least squares problem

by solving the nonsingular upper triangular system

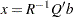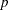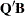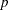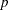then the RUPDT and RDODT subroutines can be used to update or downdate the -transformed right-hand sides and the residual sum-of-squares vector ssq provided that for each vector added to or deleted from there is also a vector 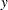added to or deleted from the 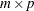right-hand-side matrix .

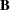If the arguments and 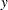of the subroutines RUPDT and RDODT contain 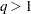row vectors for which 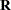(and 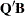, and eventually ssq) is to be updated or downdated, the process is performed stepwise by processing the rows 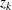(and 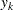), , 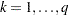in the order in which they are stored.

The QR decomposition of an 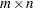matrix , , 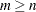rank,

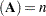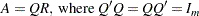corresponds to the Cholesky factorization

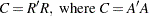of the positive definite crossproduct matrix 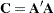. In the case where 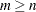and rank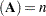, the upper triangular matrix 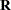computed by the QR decomposition (with positive diagonal elements) is the same as the one computed by Cholesky factorization except for numerical error,

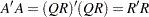Adding a row vector to matrix corresponds to the rank-1 modification of the crossproduct matrix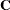

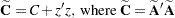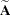and the matrix contains all rows of with the row added.

Deleting a row vector from matrix corresponds to the rank-1 modification

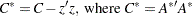and the 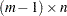matrix 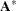contains all rows of with the row deleted. Thus, you can also use the subroutines RUPDT and RDODT to update or downdate the Cholesky factor 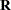of a positive definite crossproduct matrix 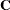of .

The process of downdating an upper triangular matrix 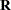(and eventually a residual sum-of-squares vector ssq) is not always successful. First of all, the downdated matrix 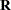could be rank deficient. Even if the downdated matrix 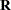is of full rank, the process of downdating can be ill-conditioned and does not work well if the downdated matrix is close (by rounding errors) to a rank-deficient one. In these cases, the downdated matrix 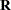is not unique and cannot be computed by subroutine RDODT. If 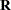cannot be computed, def returns 2, and the results rup, bup, and sup return missing values.

The downdating of the residual sum-of-squares vector ssq can be a problem, too. In practice, the downdate formula

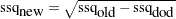cannot always be computed because, due to rounding errors, the radicand can be negative. In this case, the result vector sup returns missing values, and def returns 1.

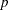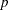You can use various methods to compute the columns of the matrix that minimize the linear least squares problems with an 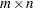coefficient matrix , , 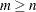rank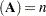, and 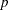right-hand-side vectors 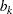(stored columnwise in the 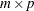matrix 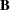). The first of the following methods solves the normal equations and cannot be applied to the example with the Hilbert matrix since too much rounding error is introduced. Therefore, use the following simple example:

    a = { 1 3 ,
          2 2 ,
          3 1 };
    b = { 1, 1, 1};
    m = nrow(a);
    n = ncol(a);
    p = 1;

• Cholesky Decomposition of Crossproduct Matrix:

     aa = a` * a; ab = a` * b;
     r  = root(aa);
     x  = trisolv(2,r,ab);
     x  = trisolv(1,r,x);
  

• QR Decomposition by Householder Transformations:

     call qr(qtb,r,piv,lindep,a, ,b);
     x = trisolv(1,r[,piv],qtb[1:n,]);
  

• Stepwise Update by Givens Rotations:

     r = j(n,n,0.); qtb = j(n,p,0.); ssq = j(1,p,0.);
     do i = 1 to m;
        z = a[i,];
        y = b[i,];
        call rupdt(rup,bup,sup,r,z,qtb,y,ssq);
        r   = rup;
        qtb = bup;
        ssq = sup;
     end;
     x = trisolv(1,r,qtb);
  

  Or equivalently:

     r   = j(n,n,0.);
     qtb = j(n,p,0.);
     ssq = j(1,p,0.);
     call rupdt(rup,bup,sup,r,a,qtb,b,ssq);
     x   = trisolv(1,rup,bup);
  

• Singular Value Decomposition:

     call svd(u,d,v,a);
     d = diag(1 / d);
     x = v * d * u` * b;
  

For the preceding 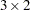example matrix , each method obtains the unique LS estimator:

   ss = ssq(a * x - b);
   print ss x;

To compute the (transposed) matrix 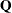, you can use the following specification:

   r = shape(0,n,n);
   y = i(m);
   qt = shape(0,n,m);
   call rupdt(rup,qtup,sup,r,a,qt,y);