| Language Reference |
| RANDGEN Call |
The RANDGEN subroutine generates random numbers from a specified distribution.
The input arguments to the RANDGEN call are as follows:
- result
is a matrix that is to be filled with random samples from the specified distribution.
- distname
is the name of the distribution that is to be sampled.
- parm1
is a distribution shape parameter.
- parm2
is a distribution shape parameter.
- parm3
is a distribution shape parameter.
The RANDGEN call generates random numbers by using the same numerical method as the RAND function in Base SAS, with the efficiency optimized for matrices. You can initialize the random number stream used by RANDGEN with the RANDSEED call. The result parameter should be preallocated to a size equal to the number of samples you want to generate. If result is not initialized, then it receives a single random sample.
The following distributions can be sampled.
Bernoulli Distribution
The random sample  is from the probability density function:
is from the probability density function:
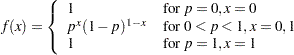 |
 is in the range:
is in the range: 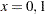
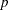 is the success probability, with range:
is the success probability, with range: 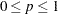
Beta Distribution
The random sample  is from the probability density function:
is from the probability density function:
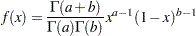 |
 is in the range:
is in the range: 
 and
and  are shape parameters, with range:
are shape parameters, with range:  and
and 
Binomial Distribution
The random sample  is from the probability density function:
is from the probability density function:
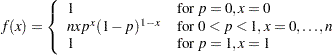 |
 is in the range:
is in the range: 
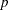 is a success probability, with range:
is a success probability, with range: 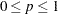
 specifies the number of independent trials, with range:
specifies the number of independent trials, with range: 
Cauchy Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 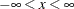
Chi-Square Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 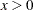
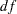 is degrees of freedom, with range:
is degrees of freedom, with range: 
Erlang Distribution
The random sample  is from the probability density function:
is from the probability density function:
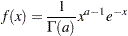 |
 is in the range:
is in the range: 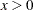
 is an integer shape parameter, with range:
is an integer shape parameter, with range: 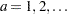
Exponential Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 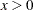
F Distribution (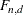 )
)
The random sample  is from the probability density function:
is from the probability density function:
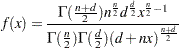 |
 is in the range:
is in the range: 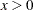
 and
and  are degrees of freedom, with range:
are degrees of freedom, with range: 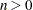 and
and 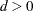
Gamma Distribution
The random sample  is from the probability density function:
is from the probability density function:
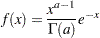 |
 is in the range:
is in the range: 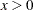
 is a shape parameter:
is a shape parameter: 
Geometric Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 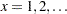
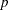 is the success probability, with range:
is the success probability, with range: 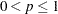
Hypergeometric Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 
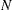 is the population size, with range:
is the population size, with range: 
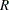 is the size of the category of interest, with range:
is the size of the category of interest, with range: 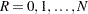
 is the sample size, with range:
is the sample size, with range: 
Lognormal Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 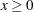
Negative Binomial Distribution
The random sample  is from the probability density function:
is from the probability density function:
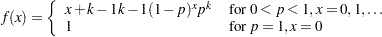 |
 is in the range:
is in the range: 
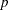 is the success probability with range:
is the success probability with range: 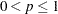
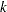 is an integer number that counts the number of successes, with range:
is an integer number that counts the number of successes, with range: 
Normal Distribution
The random sample  is from the probability density function:
is from the probability density function:
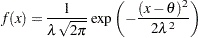 |
 is in the range:
is in the range: 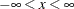
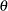 is the mean, with range:
is the mean, with range: 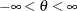 . This parameter is optional and defaults to 0.
. This parameter is optional and defaults to 0.
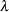 is the standard deviation, with range:
is the standard deviation, with range:  . This parameter is optional and defaults to 1.
. This parameter is optional and defaults to 1.
Poisson Distribution
The random sample  is from the probability density function:
is from the probability density function:
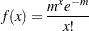 |
 is in the range:
is in the range: 
 is the mean, with range
is the mean, with range 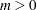
T Distribution
The random sample  is from the probability density function:
is from the probability density function:
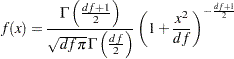 |
 is in the range:
is in the range: 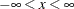
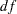 is the degrees of freedom, with the range:
is the degrees of freedom, with the range: 
Table Distribution
The random sample 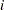 is from the probability density function:
is from the probability density function:
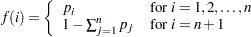 |
where 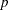 is a vector of probabilities, such that
is a vector of probabilities, such that 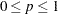 , and
, and  is the largest integer such that
is the largest integer such that  and
and
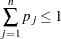 |
Triangle Distribution
The random sample  is from the probability density function:
is from the probability density function:
 |
 is in the range:
is in the range: 
 is the horizontal location of the peak of the triangle, with range:
is the horizontal location of the peak of the triangle, with range: 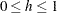
Uniform Distribution
The random sample  is from the probability density function:
is from the probability density function:
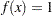 |
 is in the range:
is in the range: 
Weibull Distribution
The random sample  is from the probability density function:
is from the probability density function:
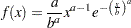 |
 is in the range:
is in the range: 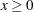
 and
and  are shape parameters, with range
are shape parameters, with range  and
and 
The following table describes how parameters of the RANDGEN call correspond to the distribution parameters.
Distribution |
distname |
parm1 |
parm2 |
parm3 |
|---|---|---|---|---|
Bernoulli |
’BERNOULLI’ |
|
||
Beta |
’BETA’ |
|
|
|
Binomial |
’BINOMIAL’ |
|
|
|
Cauchy |
’CAUCHY’ |
|||
Chi-Square |
’CHISQUARE’ |
|
||
Erlang |
’ERLANG’ |
|
||
Exponential |
’EXPONENTIAL’ |
|||
|
’F’ |
|
|
|
Gamma |
’GAMMA’ |
|
||
Geometric |
’GEOMETRIC’ |
|
||
Hypergeometric |
’HYPERGEOMETRIC’ |
|
|
|
Lognormal |
’LOGNORMAL’ |
|||
Negative Binomial |
’NEGBINOMIAL’ |
|
|
|
Normal |
’NORMAL’ |
|
|
|
Poisson |
’POISSON’ |
|
||
T |
’T’ |
|
||
Table |
’TABLE’ |
|
||
Triangle |
’TRIANGLE’ |
|
||
Uniform |
’UNIFORM’ |
|||
Weibull |
’WEIBULL’ |
|
|
In practice, distname can be in lowercase or uppercase, and you only need to specify enough letters to distinguish one distribution from the others. For example,
/* generate 10 samples from a Bernoulli distribution */ r = j(10, 1, .); /* allocate room for samples */ call randgen(r,"ber",p);
Except for the normal distribution, you must specify the parameters listed for each of the preceding distributions. For the normal distribution, default values of 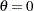 and
and 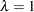 are used if none are supplied.
are used if none are supplied.
The following example illustrates the use of the RANDGEN call.
call randseed(12345);
/* get four random observations from each distribution */
x = j(1, 4, .);
/* each row of m comes from a different distribution */
m = j(20, 4, .);
call randgen(x, 'BERN', 0.75);
m[1, ] = x;
call randgen(x, 'BETA', 3, 0.1);
m[2, ] = x;
call randgen(x, 'BINOM', 10, 0.75);
m[3, ] = x;
call randgen(x, 'CAUCHY');
m[4, ] = x;
call randgen(x, 'CHISQ', 22);
m[5, ] = x;
call randgen(x, 'ERLANG', 7);
m[6, ] = x;
call randgen(x, 'EXPO');
m[7, ] = x;
call randgen(x, 'F', 12, 322);
m[8, ] = x;
call randgen(x, 'GAMMA', 7.25);
m[9, ] = x;
call randgen(x, 'GEOM', 0.02);
m[10, ] = x;
call randgen(x, 'HYPER', 10, 3, 5);
m[11, ] = x;
call randgen(x, 'LOGN');
m[12, ] = x;
call randgen(x, 'NEGB', 0.8, 5);
m[13, ] = x;
call randgen(x, 'NORMAL'); /* default parameters */
m[14, ] = x;
call randgen(x, 'POISSON', 6.1);
m[15, ] = x;
call randgen(x, 'T', 4);
m[16, ] = x;
p = {0.1 0.2 0.25 0.1 0.15 0.1 0.1};
call randgen(x, 'TABLE', p);
m[17, ] = x;
call randgen(x, 'TRIANGLE', 0.7);
m[18, ] = x;
call randgen(x, 'UNIFORM');
m[19, ] = x;
call randgen(x, 'WEIB', 0.25, 2.1);
m[20, ] = x;
print m;
The output is as follows:
M
1 0 1 0
1 0.9999234 0.9842784 0.9997739
7 8 5 10
-1.209834 3.9732282 -0.048339 -1.337284
30.300691 20.653151 27.301922 26.878221
10.636299 4.6455449 7.5284821 2.5558646
0.2449632 2.7656037 4.2254588 0.2866158
0.7035829 1.2676112 0.9806787 1.4811389
8.475216 8.8723256 8.2993617 8.0409742
109 4 33 30
1 1 2 1
0.7784513 0.9792472 0.6018993 0.3643607
3 2 0 2
0.0053637 1.4026784 -0.271338 -0.416685
5 11 8 4
1.3237918 0.0505162 -0.660845 -0.634447
2 3 2 3
0.5270875 0.6909336 0.8607548 0.5450831
0.4064393 0.7464901 0.3463207 0.2615394
0.4183405 0.9981923 16.812803 0.0001131
Copyright © SAS Institute, Inc. All Rights Reserved.