| Language Reference |
| NLPNRA Call |
See the section Nonlinear Optimization and Related Subroutines for a listing of all NLP subroutines. See Chapter 14 for a description of the arguments of NLP subroutines.
The NLPNRA algorithm uses a pure Newton step at each iteration when both the Hessian is positive definite and the Newton step successfully reduces the value of the objective function. Otherwise, it performs a combination of ridging and line-search to compute successful steps. If the Hessian is not positive definite, a multiple of the identity matrix is added to the Hessian matrix to make it positive definite (see Eskow and Schnabel (1991)).
The subroutine uses the gradient 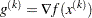 and the Hessian matrix
and the Hessian matrix
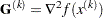 , and it requires continuous first- and second-order derivatives of the objective function inside the feasible region. If second-order derivatives are computed efficiently and precisely, the NLPNRA method does not need many function, gradient, and Hessian calls, and it can perform well for medium to large problems.
, and it requires continuous first- and second-order derivatives of the objective function inside the feasible region. If second-order derivatives are computed efficiently and precisely, the NLPNRA method does not need many function, gradient, and Hessian calls, and it can perform well for medium to large problems.
Note that using only function calls to compute finite difference approximations for second-order derivatives can be computationally very expensive and can contain significant rounding errors. If you use the "grd" input argument to specify a module that computes first-order derivatives analytically, you can reduce drastically the computation time for numerical second-order derivatives. The computation of the finite difference approximation for the Hessian matrix generally uses only  calls of the module that specifies the gradient.
calls of the module that specifies the gradient.
In each iteration, a line search is done along the search direction to find an approximate optimum of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation. You can specify other line-search algorithms with the fifth element of the opt argument. See the section Options Vector for details.
In unconstrained and boundary constrained cases, the NLPNRA algorithm can take advantage of diagonal or sparse Hessian matrices that are specified by the input argument "hes". To use sparse Hessian storage, the value of the ninth element of the opt argument must specify the number of nonzero Hessian elements returned by the Hessian module. See the section Objective Function and Derivatives for more details.
In addition to the standard iteration history, the NLPNRA subroutine prints the following information:
The heading alpha is the step size,
 , computed with the line-search algorithm.
, computed with the line-search algorithm. The heading slope refers to
 , the slope of the search direction at the current parameter iterate
, the slope of the search direction at the current parameter iterate  . For minimization, this value should be significantly smaller than zero. Otherwise, the line-search algorithm has difficulty reducing the function value sufficiently.
. For minimization, this value should be significantly smaller than zero. Otherwise, the line-search algorithm has difficulty reducing the function value sufficiently.
The following statements invoke the NLPNRA subroutine to solve the constrained Betts optimization problem (see the section Constrained Betts Function). The iteration history follows.
start F_BETTS(x);
f = .01 * x[1] * x[1] + x[2] * x[2] - 100;
return(f);
finish F_BETTS;
con = { 2 -50 . .,
50 50 . .,
10 -1 1 10};
x = {-1 -1};
optn = {0 2};
call nlpnra(rc, xres, "F_BETTS", x, optn, con);
| Note: | Initial point was changed to be feasible for boundary and linear constraints. |
| Test of NLPHQN subroutine: No Derivatives |
| Optimization Start | |||||
|---|---|---|---|---|---|
| Parameter Estimates | |||||
| N | Parameter | Estimate | Gradient Objective Function |
Lower Bound Constraint |
Upper Bound Constraint |
| 1 | X1 | 6.800000 | 0.136000 | 2.000000 | 50.000000 |
| 2 | X2 | -1.000000 | -2.000000 | -50.000000 | 50.000000 |
| Linear Constraints | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 59.00000 | : | 10.0000 | <= | + | 10.0000 | * | X1 | - | 1.0000 | * | X2 | |
| Test of NLPHQN subroutine: No Derivatives |
| Parameter Estimates | 2 |
|---|---|
| Lower Bounds | 2 |
| Upper Bounds | 2 |
| Linear Constraints | 1 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Step Size |
Slope of Search Direction |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 0 | -98.81551 | 0.2779 | 1.8000 | 0.100 | -2.925 | ||
| 2 | * | 0 | 3 | 0 | -99.40840 | 0.5929 | 1.2713 | 0.294 | -2.365 | |
| 3 | * | 0 | 4 | 1 | -99.87460 | 0.4662 | 0.5845 | 0.540 | -1.182 | |
| 4 | 0 | 5 | 1 | -99.96000 | 0.0854 | 0.000025 | 1.000 | -0.171 | ||
| 5 | 0 | 6 | 1 | -99.96000 | 1.54E-10 | 0 | 1.000 | -31E-11 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 5 | Function Calls | 7 |
| Hessian Calls | 6 | Active Constraints | 1 |
| Objective Function | -99.96 | Max Abs Gradient Element | 0 |
| Slope of Search Direction | -3.07388E-10 | Ridge | 0 |
Copyright © SAS Institute, Inc. All Rights Reserved.