| Language Reference |
| MAXQFORM Call |
The MAXQFORM subroutine computes the subsets of a matrix system that maximize the quadratic form.
If 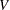 and
and  are an
are an  matrix and an
matrix and an 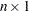 vector, respectively, then the MAXQFORM function computes the subsets of components
vector, respectively, then the MAXQFORM function computes the subsets of components  such that
such that  is maximized.
is maximized.
The MAXQFORM subroutine returns the following values:
- rc
is one of the following scalar return codes:
0
normal return
1
error: the number of elements of
 is too large to process
is too large to process 2
error:
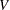 is not positive semidefinite
is not positive semidefinite - maxq
is an
 matrix, where
matrix, where  is the total number of subsets computed and
is the total number of subsets computed and  is the number of elements in
is the number of elements in  . The value of
. The value of  depends on the value of best and is equal to
depends on the value of best and is equal to 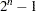 if best is not specified. Each row of maxq contains information for a selected subset of
if best is not specified. Each row of maxq contains information for a selected subset of 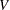 and
and  . The first element of the row is the number of components in the subset. The second element is the value of the quadratic form. The following elements of the row are either 0 or 1, to indicate whether the corresponding components of
. The first element of the row is the number of components in the subset. The second element is the value of the quadratic form. The following elements of the row are either 0 or 1, to indicate whether the corresponding components of 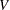 and
and  are included in the subset.
are included in the subset.
The input arguments to the MAXQFORM subroutine are as follows:
- V
specifies an
 positive semidefinite matrix. Often this is generated as a crossproduct matrix,
positive semidefinite matrix. Often this is generated as a crossproduct matrix,  , where
, where 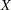 is a
is a 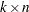 matrix.
matrix. - b
specifies an
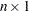 vector. Often this arises as
vector. Often this arises as 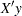 , where
, where 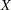 is a
is a 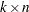 matrix, and
matrix, and 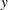 is a
is a 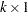 vector.
vector. - best
specifies an optional scalar. If best is specified with the value
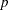 , then the
, then the 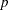 subsets with the largest value for the quadratic form are returned for each subset size.
subsets with the largest value for the quadratic form are returned for each subset size.
The leaps and bounds algorithm by Furnival and Wilson (1974) computes the maximum value of quadratic forms for subsets of components. Many statistics computed as a quadratic form can then be used as the criterion for the method of subset selection. These include the regression sum of squares, Wald statistics, and score statistics.
Consider the following fitness data, which consists of observations with values for age measured in years, weight measured in kilograms, time to run 1.5 miles measured in minutes, heart rate while resting, heart rate while running, maximum heart rate recorded while running, and oxygen intake rate while running measured in milliliters per kilogram of body weight per minute.
fit = {
44 89.47 11.37 62 178 182 44.609,
40 75.07 10.07 62 185 185 45.313,
44 85.84 8.65 45 156 168 54.297,
42 68.15 8.17 40 166 172 59.571,
38 89.02 9.22 55 178 180 49.874,
47 77.45 11.63 58 176 176 44.811,
40 75.98 11.95 70 176 180 45.681,
43 81.19 10.85 64 162 170 49.091,
44 81.42 13.08 63 174 176 39.442,
38 81.87 8.63 48 170 186 60.055,
44 73.03 10.13 45 168 168 50.541,
45 87.66 14.03 56 186 192 37.388,
45 66.45 11.12 51 176 176 44.754,
47 79.15 10.60 47 162 164 47.273,
54 83.12 10.33 50 166 170 51.855,
49 81.42 8.95 44 180 185 49.156,
51 69.63 10.95 57 168 172 40.836,
51 77.91 10.00 48 162 168 46.672,
48 91.63 10.25 48 162 164 46.774,
49 73.37 10.08 67 168 168 50.388,
57 73.37 12.63 58 174 176 39.407,
54 79.38 11.17 62 156 165 46.080,
52 76.32 9.63 48 164 166 45.441,
50 70.87 8.92 48 146 155 54.625,
51 67.25 11.08 48 172 172 45.118,
54 91.63 12.88 44 168 172 39.203,
51 73.71 10.47 59 186 188 45.790,
57 59.08 9.93 49 148 155 50.545,
49 76.32 9.40 56 186 188 48.673,
48 61.24 11.50 52 170 176 47.920,
52 82.78 10.50 53 170 172 47.467 };
Use the following statement to center the data:
fitc = fit - fit[:,];
Now compute the crossproduct matrices, as follows:
x = fitc[, 1:6]; y = fitc[, 7]; xpx = x`*x; xpy = x`*y;
The following statements compute the best three regression sums of squares for each size of regressor set:
call maxqform(rc, maxq, xpx, xpy, 3); print maxq;
| maxq | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 632.9001 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 135.78285 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 134.84474 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 650.66573 | 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 648.26218 | 0 | 0 | 1 | 0 | 1 | 0 |
| 2 | 634.46746 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 690.55086 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 689.60921 | 0 | 0 | 1 | 0 | 1 | 1 |
| 3 | 665.55064 | 1 | 0 | 1 | 0 | 0 | 1 |
| 4 | 712.45153 | 1 | 0 | 1 | 0 | 1 | 1 |
| 4 | 695.14669 | 1 | 1 | 1 | 0 | 1 | 0 |
| 4 | 694.5988 | 0 | 1 | 1 | 0 | 1 | 1 |
| 5 | 721.97309 | 1 | 1 | 1 | 0 | 1 | 1 |
| 5 | 712.63302 | 1 | 0 | 1 | 1 | 1 | 1 |
| 5 | 696.05218 | 1 | 1 | 1 | 1 | 1 | 0 |
| 6 | 722.54361 | 1 | 1 | 1 | 1 | 1 | 1 |
Copyright © SAS Institute, Inc. All Rights Reserved.